Multilevel Generalized Linear Models

Prof. Maria Tackett

Apr 01, 2024

Announcements

  • Project 02

    • Presentations April 3 during lecture
    • Written report + GitHub repo due April 4 at 11:59pm

  • Looking ahead:

    • HW 05 released on Thursday

    • No office hours or lecture on Monday, April 8

  • Final project - Round 1 submission (optional) due April 25

Topics

  • Exploratory data analysis for multilevel data with non-normal response variable

  • Use a two-stage modeling approach to understand conclusions at each level

  • Write Level One, Level Two and composite models for mutlilevel GLM

  • Fit and interpret multilevel GLM

Data: College Basketball referees

Today’s data set includes information on 4972 fouls in 340 NCAA basketball games from the Big Ten, ACC, and Big East conferences during the 2009-2010 season. The goal is to determine whether the data from this season support a conclusion from Anderson and Pierce (2009) that referees tend to “even out” foul calls in a game. The variables we’ll focus on are

  • foul.home: foul was called on home team (1: yes, 0: no)
  • foul.diff: difference in fouls before current foul was called (home - visitor)
  • game: Unique game ID number
  • visitor: visiting team abbreviation
  • home: home team abbreviation

See BMLR: Section 11.3.1 for full codebook.

Data: College basketball referees

game visitor hometeam foul.num foul.home foul.vis foul.diff foul.type time
1 IA MN 1 0 1 0 Personal 14.167
1 IA MN 2 1 0 -1 Personal 11.433
1 IA MN 3 1 0 0 Personal 10.233
1 IA MN 4 0 1 1 Personal 9.733
1 IA MN 5 0 1 0 Shooting 7.767
1 IA MN 6 0 1 -1 Shooting 5.567
1 IA MN 7 1 0 -2 Shooting 2.433
1 IA MN 8 1 0 -1 Offensive 1.000
2 MI MIST 1 0 1 0 Shooting 18.983
2 MI MIST 2 1 0 -1 Personal 17.200

Modeling approach

  • foul.home is a binary response variable (1: foul called on home team, 0: foul called on visiting team)

    ✅ Use a generalized linear model, specifically one with the logit link function

  • Data has a multilevel structure

    • Covariates at individual foul level and game level

      ✅ Use a multilevel model

We will combine these and fit a multilevel generalized linear model with a logit link function

Exploratory data analysis

Exploratory data analysis

Univariate

  • Visualizations and summary statistics for Level One and Level Two variables

Bivariate

  • Segmented bar plots or mosaic plots for response vs. categorical predictors

  • Conditional density plot for response vs. quantitative predictors

  • Empirical logit plot for quantitative predictors

    • Is relationship reasonably linear?

Application exercise

📋 sta310-sp24.netlify.app/ae/lec-20-mutlievel-glm

06:00

Logistic regression

Start with a logistic regression model treating all observations as independent

Quick analysis to get initial intuition about research question sand important variables, not for final conclusions

term estimate std.error statistic p.value
(Intercept) -0.103 0.101 -1.023 0.306
foul.diff -0.077 0.025 -3.078 0.002
score.diff 0.020 0.007 3.012 0.003
lead.home -0.093 0.160 -0.582 0.560
time -0.013 0.008 -1.653 0.098
foul.diff:time -0.007 0.003 -2.485 0.013
lead.home:time 0.022 0.011 1.957 0.050

Two-stage modeling

Two-stage modeling

For now, let’s fit a model focusing on the question: Do the data provide evidence that referees tend to “even out” fouls?

To explore this, we will fit a model with the Level One predictor foul.diff using a two-stage modeling approach.

Two-stage modeling approach

  • Fit a separate model of the association between foul.diff and foul.home for each game (Level One models)

  • Fit models to explain game-to-game variability in the estimated slopes and intercepts (Level Two models)

Model set up

  • \(Y_{ij}\): 1 if \(j^{th}\) foul in Game \(i\) was called on home team; 0 otherwise.
  • \(p_{ij}\): True probability the \(j^{th}\) foul in Game \(i\) was called on home team

\[ Y_{ij} \sim Bernoulli(p_{ij}) \]

Model Set Up

Level One models

\[\log\Big(\frac{p_{ij}}{1 - p_{ij}}\Big) = a_i + b_i ~ \text{foul.diff}_{ij}\]


Level Two models

Explain the game-to-game variability in the intercepts (\(a_i\)) and the slopes (\(b_i\))

Level One Models

For Game 1

level_one_model <- basketball |>
  filter(game == 1) |>
  glm(factor(foul.home) ~ foul.diff, data = _, family = binomial)

tidy(level_one_model) |> kable(digits = 3)
term estimate std.error statistic p.value
(Intercept) -0.951 1.110 -0.857 0.392
foul.diff -1.901 1.369 -1.389 0.165

For Game 2

level_one_model <- basketball |> 
  filter(game == 2) |> 
  glm(factor(foul.home) ~ foul.diff, data = _, family = binomial)
tidy(level_one_model) |> kable(digits = 3)
term estimate std.error statistic p.value
(Intercept) 2.047 1.424 1.438 0.150
foul.diff -0.780 0.525 -1.486 0.137

Level One Models

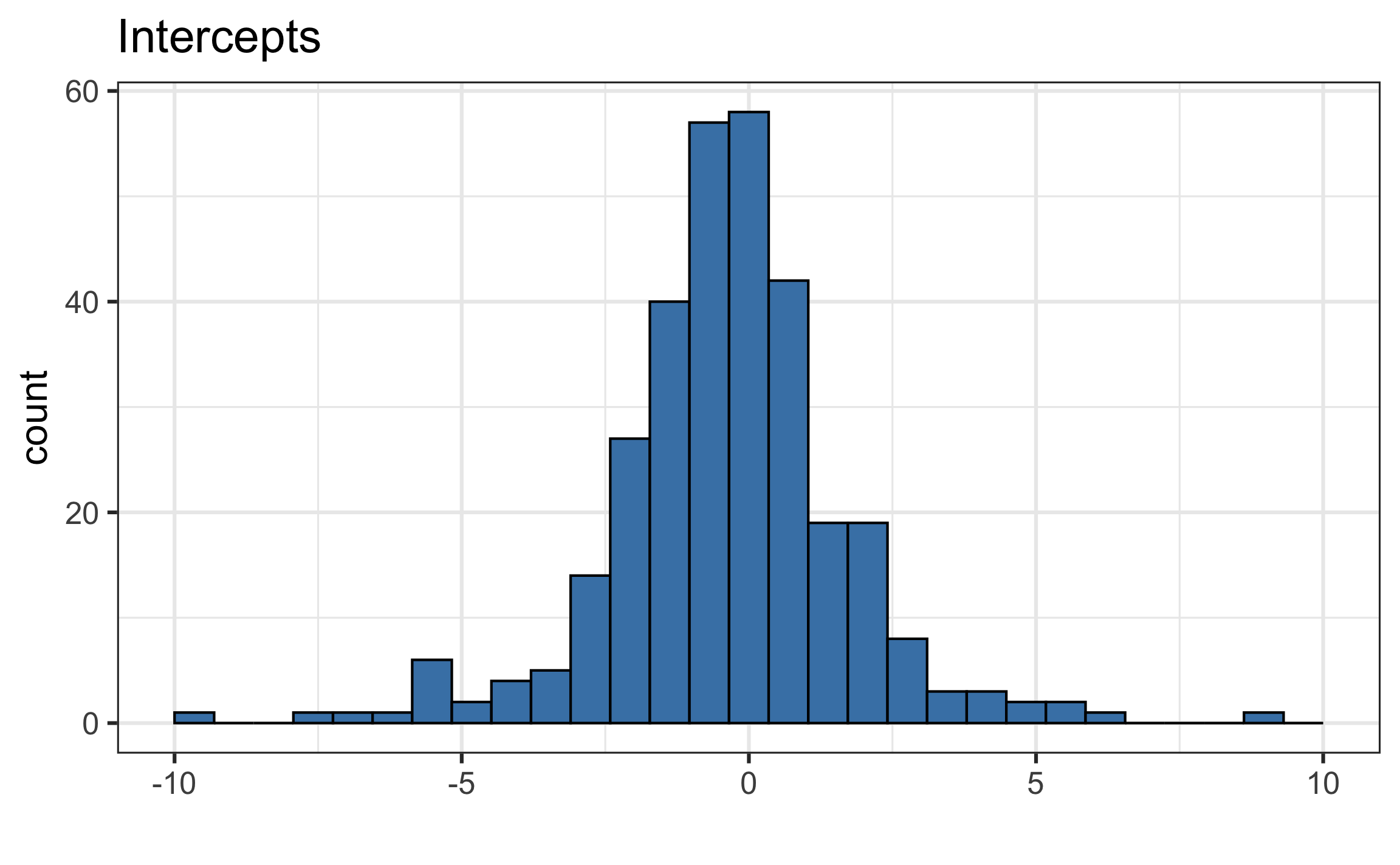
alpha0 sigma2_u
-0.301 128.858

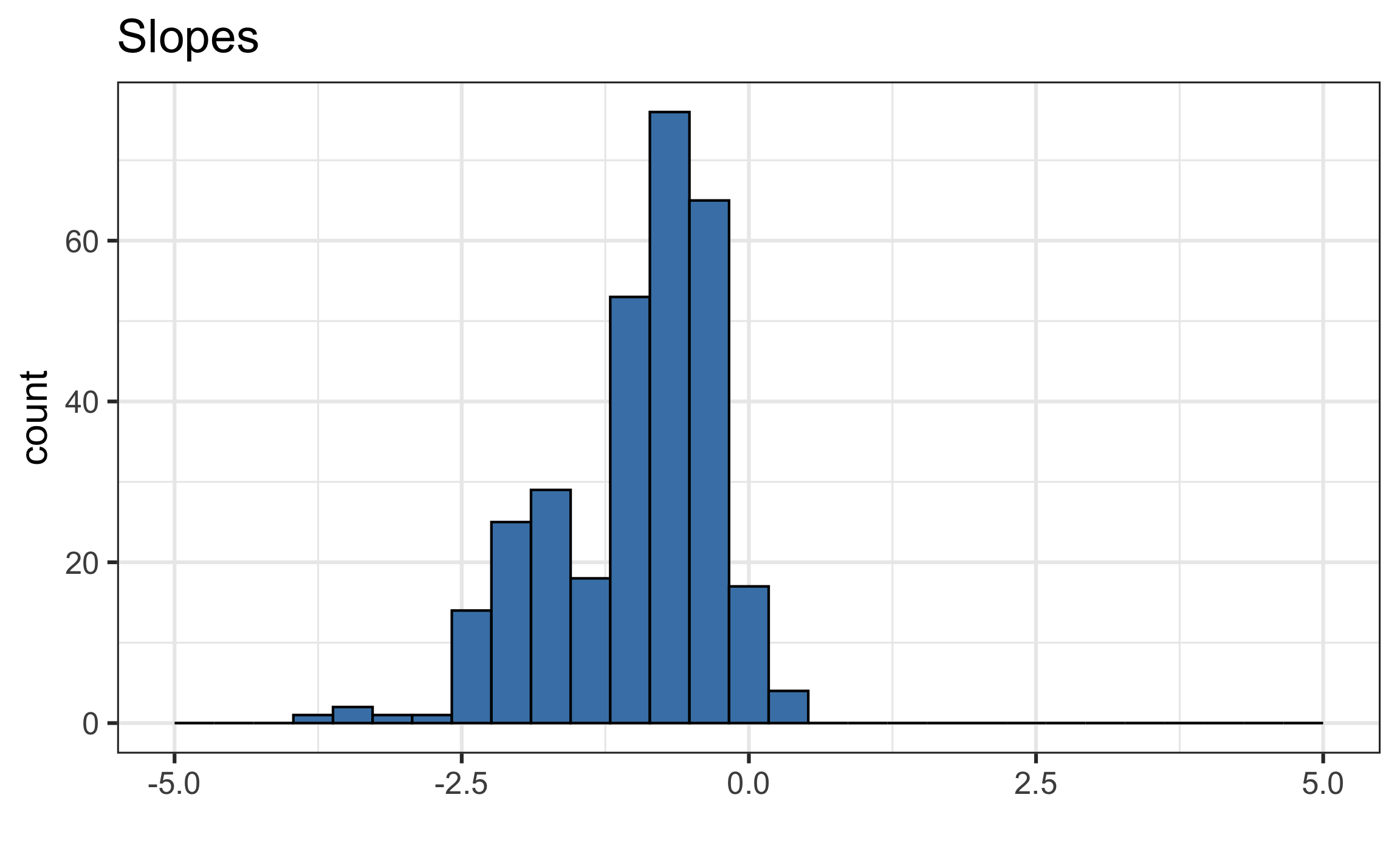
beta0 sigma2_v
-3.328 60.049


What do we learn from the distribution of the slopes and intercepts?

Consider number of fouls per game

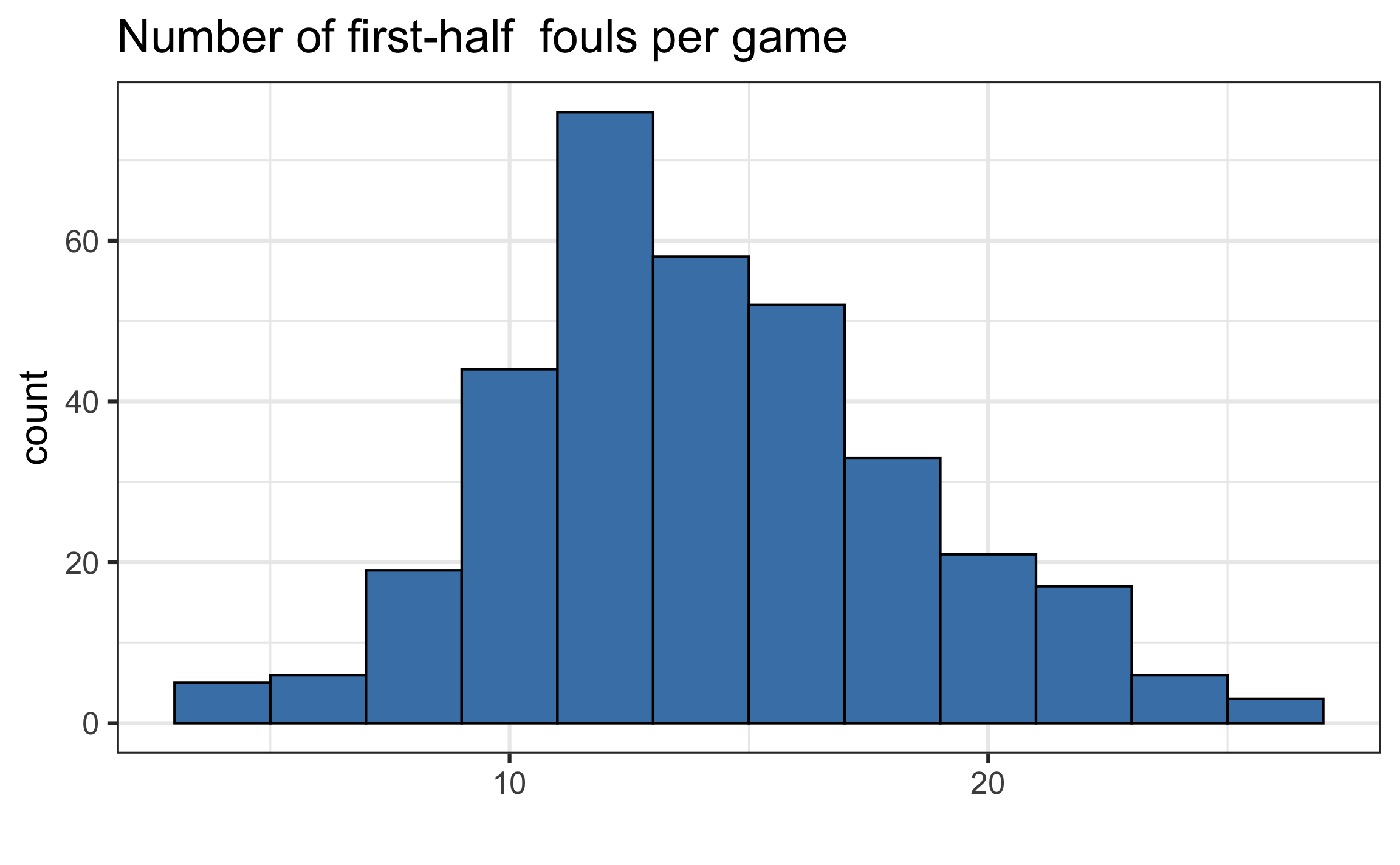
Warning

In the two-stage approach, games with 3 fouls are treated with equal weight as games with 20 + fouls

Unified multilevel model

Models by level

Level One models

\[\log\Big(\frac{p_{ij}}{1 - p_{ij}}\Big) = a_i + b_i ~ \text{foul.diff}_{ij}\] Level Two models

\[a_i = \alpha_0 + u_i\hspace{20mm} b_i = \beta_0 + v_i\]

\[\left[ \begin{array}{c} u_i \\ v_i \end{array} \right] \sim N \left( \left[ \begin{array}{c} 0 \\ 0 \end{array} \right], \left[ \begin{array}{cc} \sigma_u^{2} & \sigma_{uv} \\ \sigma_{uv} & \sigma_{v}^{2} \end{array} \right] \right)\]

Composite model

Composite model \[\log\Big(\frac{p_{ij}}{1 - p_{ij}}\Big) = \alpha_0 + \beta_0 ~ \text{foul.diff}_{ij} + [u_i + v_i ~ \text{foul.diff}_{ij}]\] \[\left[ \begin{array}{c} u_i \\ v_i \end{array} \right] \sim N \left( \left[ \begin{array}{c} 0 \\ 0 \end{array} \right], \left[ \begin{array}{cc} \sigma_u^{2} & \sigma_{uv} \\ \sigma_{uv} & \sigma_{v}^{2} \end{array} \right] \right)\]

Fit the model in R

Use the glmer function in the lme4 package to fit multilevel GLMs.

model1 <- glmer(foul.home ~ foul.diff + (foul.diff|game), 
                data = basketball, family = binomial)
boundary (singular) fit: see help('isSingular')
effect group term estimate std.error statistic p.value
fixed NA (Intercept) -0.157 0.046 -3.382 0.001
fixed NA foul.diff -0.285 0.038 -7.440 0.000
ran_pars game sd__(Intercept) 0.542 NA NA NA
ran_pars game cor__(Intercept).foul.diff -1.000 NA NA NA
ran_pars game sd__foul.diff 0.035 NA NA NA

Boundary constraints

Boundary constraints

  • The estimates of the parameters \(\alpha_0, \beta_0, \sigma_u, \sigma_v, \rho_{uv}\) are those that maximize the likelihood of observing the data

  • The fixed effects, e.g., \(\alpha_0\) and \(\beta_0\), can take any values, but the terms associated with the error terms are constrained to a set of “allowable” values

    • \[\sigma_u \geq 0 \hspace{10mm} \sigma_v \geq 0 \hspace{10mm} -1 \leq \rho_{uv} \leq 1\]

  • Because of these boundaries, a “constrained” search is used to find the MLEs.

  • The error message "## boundary (singular) fit", means the estimate of one or more terms was set at the maximum (or minimum) allowable value, not the value it would’ve been if an unconstrained search were allowable

Illustrating boundary constraints

Contour plots from a hypothetical likelihood \(L(\beta_0, \sigma^2)\)


From BMLR Figure 10.14

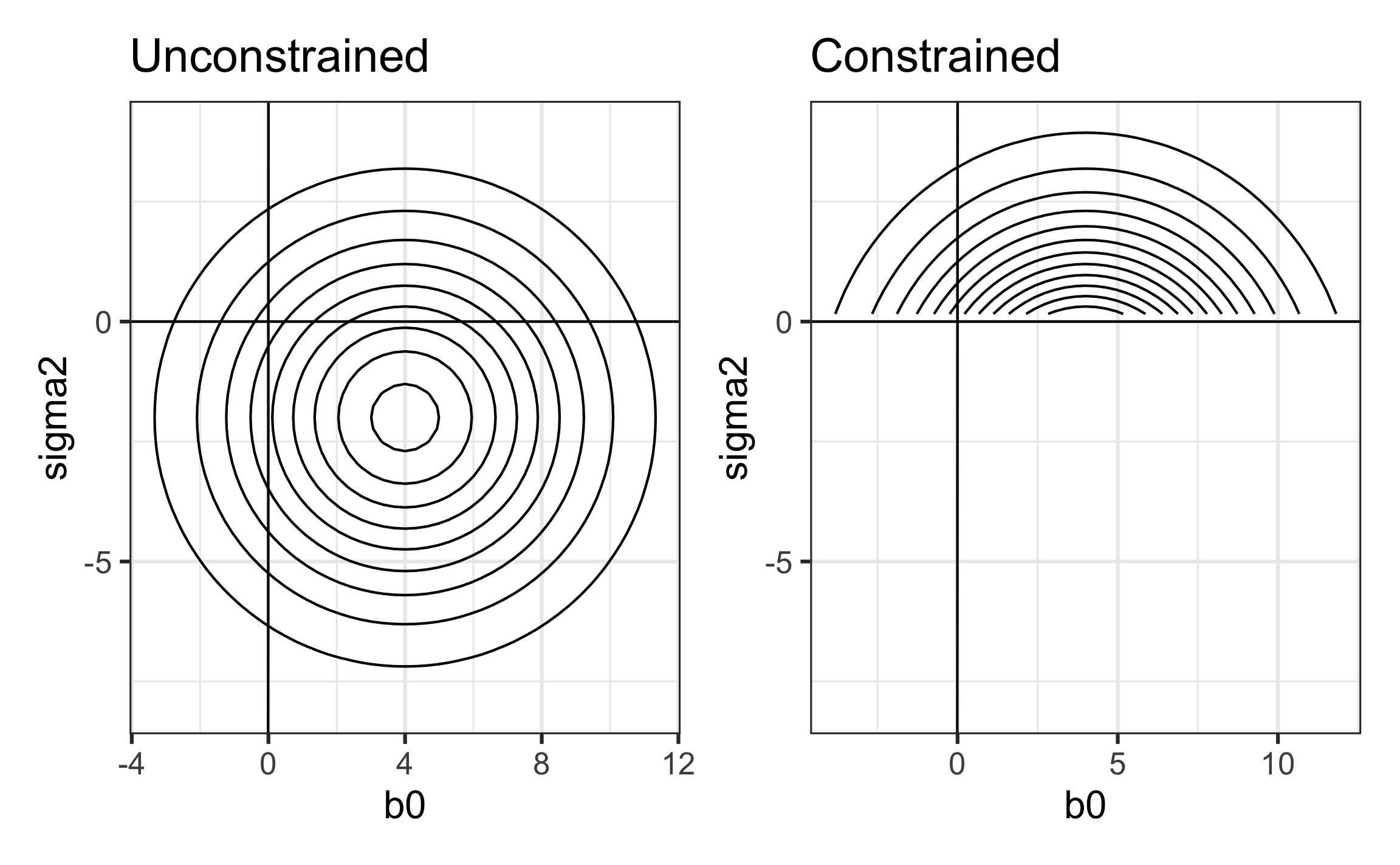
  • In the unconstrained search, the likelihood \(L(\beta_0, \sigma^2)\) is maximized at \(\hat{\beta}_0 = 4, \hat{\sigma}^2 = -2\)

  • In reality \(\sigma^2\) must be non-negative, so the search for the MLE is restricted to the region such that \(\sigma^2 \geq 0\).

  • The constrained likelihood is maximized at \(\hat{\beta}_0 = 4, \hat{\sigma}^2 = 0\)

Addressing boundary constraints

Address boundary constraints by reparameterizing the model

  • Remove variance and/or correlation terms estimated at the boundary

  • Reduce the number of parameters to be estimated by fixing the values of some parameters

  • Apply transformation to covariates, such as centering variables, standardizing variables, or changing units. Extreme values, outliers, or highly correlated covariates can sometimes cause issues with MLEs.

Is it OK to use model that faces boundary constraints?

Best to try to deal with boundary constraints, but you can sometimes leave the model as is if…

  • You’re not interested in estimating parameters with boundary issues

  • Removing the parameters does not impact conclusions about the variables of interest

Original model

effect group term estimate std.error statistic p.value
fixed NA (Intercept) -0.157 0.046 -3.382 0.001
fixed NA foul.diff -0.285 0.038 -7.440 0.000
ran_pars game sd__(Intercept) 0.542 NA NA NA
ran_pars game cor__(Intercept).foul.diff -1.000 NA NA NA
ran_pars game sd__foul.diff 0.035 NA NA NA


  1. Which term(s) should we remove to try to address boundary constraint?
  2. Refit the model with these terms removed. 3. Which model do you choose? Explain.
04:00

Interpret model coefficients

Interpret the following coefficients in the selected model (if applicable):

  • \(\hat{\alpha}_0\)

  • \(\hat{\beta}_0\)

  • \(\hat{\sigma}_u\)

  • \(\hat{\sigma}_v\)

  • \(\hat{\rho}_{uv}\)

Looking ahead

So far we’ve only considered random effects within a nested structure, but sometimes we may want to consider random effects that aren’t nested.

  • For example, we want to consider a random effect for the home team, but home team is not nested within game (since teams can be the home team for multiple games)

  • We will deal with this using crossed random effects

References

🔗 STA 310 - Spring 2024

Anderson, Kyle J, and David A Pierce. 2009. “Officiating Bias: The Effect of Foul Differential on Foul Calls in NCAA Basketball.” Journal of Sports Sciences 27 (7): 687–94.
Roback, Paul, and Julie Legler. 2021. Beyond multiple linear regression: applied generalized linear models and multilevel models in R. CRC Press.