Modeling data with three (or more) levels

Prof. Maria Tackett

Mar 25, 2024

Announcements

  • Quiz 04 - March 26 ~ 9am - March 28 at noon

    • Covers readings and lectures March 4 - 20

    • Longitudinal modeling, Chapter 9 of BMLR

  • Project 02

    • Presentations April 3 during lecture
    • Written report + GitHub repo due April 4 at 11:59pm

  • Final project - Round 1 submission (optional) due April 25

Topics

  • Write form of model for models with more than two levels

  • Interpret fixed and random effects at each level

  • See how three-level models are used in data analysis example

Note

The notes are based on Chapter 10 of Roback and Legler (2021) and Jones (1991) unless otherwise noted.

Sleep study

Data structure

Let’s look at the study about the effect of sleep on quality of life indicators. The data follow a multilevel structure with 3 levels

  • Level Three: Household

    • Level Two: Individual

      • Level One: Wave

Outcomes of interest

We will focus on three of the outcomes:

  • Life satisfaction (lfstat_OT): “represents a stable assessment of general feelings about life and indicates a long-term attitude”

    • Measured as response, ranging from 0 (extremely dissatisfied) to 10 (extremely satisfied), to the question “All things considered, how satisfied are you with your life as a whole?”

  • Wellbeing (wellbe_OT): “captures a person’s emotional state and touches on their mental state”

    • Measured as average response, ranging from “at no time” to “all of the time”, to three items about how often in the last two weeks respondents “have been cheerful and in good spirits”, “have felt calm and relaxed”, and “have been active and vigorous”

Outcomes of interest

  • Happiness (happy_OT): a person’s current positive emotional condition

    • Measured as response, ranging from 0 (extremely unhappy) to 10 (extremely happy), to the question “Taking all things together, how happy would you say you are?”

Sleep variables

  • sleep duration (SDweek_OT)

  • quality of sleep (slequal_OT)

  • social jetlag (jetlag_OT)

Other covariates

  • sex
  • highest level of education attained (basic and secondary vocational, secondary with maturita, tertiary education)
  • household income (divided into 6 categories)
  • age
  • employment status (employed, self-employed, unemployed, student, retired, on maternity leave)
  • number of children below age 5 in the household
  • wave (2018, 2019, 2020)

Conclusions

Recall the Modeling section in the lec-17 AE.

What are your conclusions about the effects of sleep on quality of life indicators?

Limitations

What are some potential limitations of this study?

Modeling data with three (or more) levels

Data: Housing prices in Southampton

The data includes the price and characteristics for 918 houses sold between 1986 and 1991 in Southampton, England. The data were originally collected from a local real estate agency and were analyzed in Jones (1991). The primary variables of interest are

  • price: Sales price in thousands of £
  • Age: Age of the house
  • Bedrooms: Number of bedrooms
  • House Type: (semi-detached, detached, bungalow, terrace, flat)
  • Central heating: Whether house has central heating (0: yes, 1: no)
  • Garage: Number of garages (none, single, double)
  • Districts: one of 34 districts
  • Half-years: Half-year periods beginning the second half of 1986

Data structure

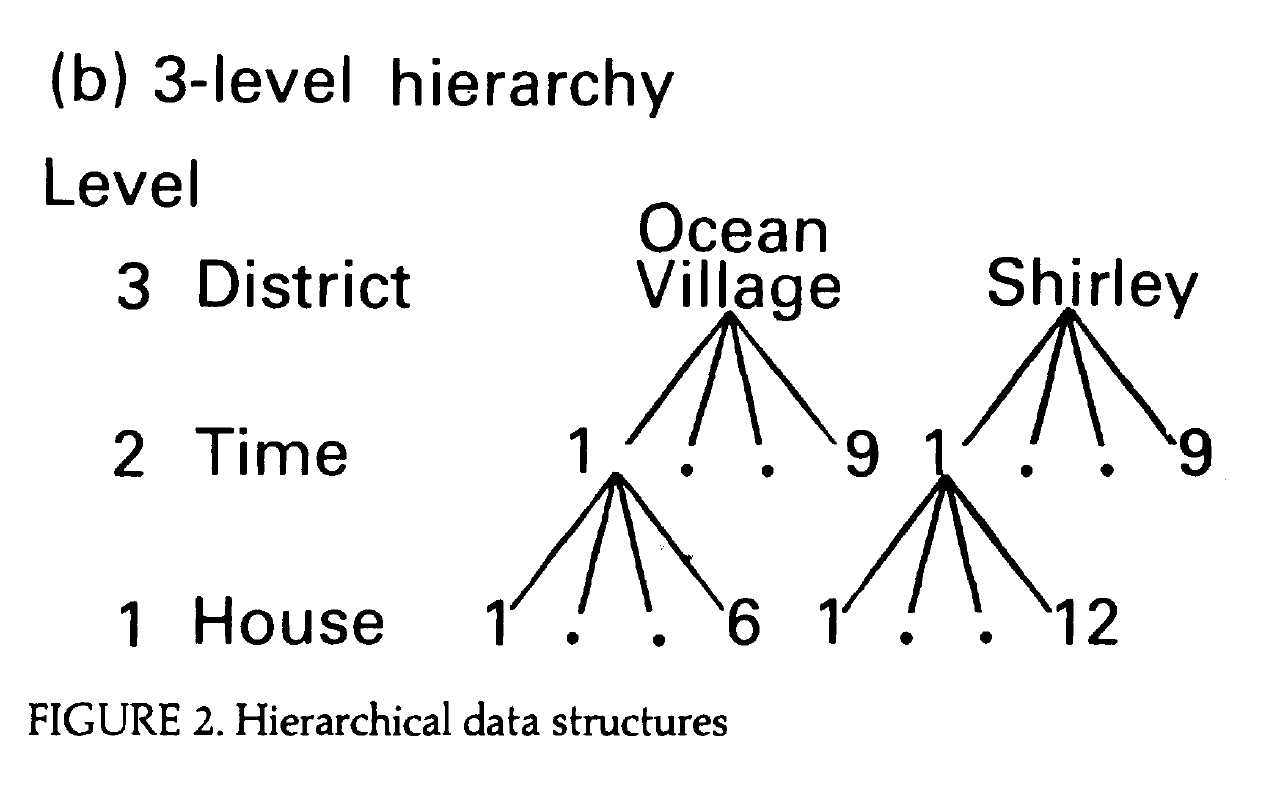
Portions of Figure 2b from Jones (1991)

Note

You can access the paper on Canvas.The paper uses different symbols to represent parameters than what is in the textbook. The slides will follow the textbook.

Unconditional means model

\[ Y_{ijk} = \alpha_0 + \tilde{u}_i + u_{ij} + \epsilon_{ijk} \]

Level One (house within time)

\(Y_{ijk} = a_{ij} + \epsilon_{ijk}, \hspace{10mm} \epsilon_{ijk} \sim N(0, \sigma^2)\)

Level Two (time within district)

\(a_{ij} = a_i + u_{ij}, \hspace{10mm} u_{ij} \sim N(0, \sigma^2_u)\)

Level Three (district)

\(a_{i} = \alpha_0 + \tilde{u}_{i}, \hspace{10mm} \tilde{u}_{i} \sim N(0, \sigma^2_{\tilde{u}})\)

Label the terms of the composite model

  • \(Y_{ijk}\): Price of house \(k\) in district \(i\) sold in time period \(j\)

  • \(\alpha_0\):

  • \(\epsilon_{ijk}\):

  • \(u_{ij}\)

  • \(\tilde{u}_i\):

  • \(\sigma\): Variance component describing house-to-house variability within a given time period

  • \(\sigma_{u}\): Variance component describing variability between time periods within a district

  • \(\sigma_{\tilde{u}}\): Variance component describing district-to-district variability

Model A

Table 1 from Jones (1991)


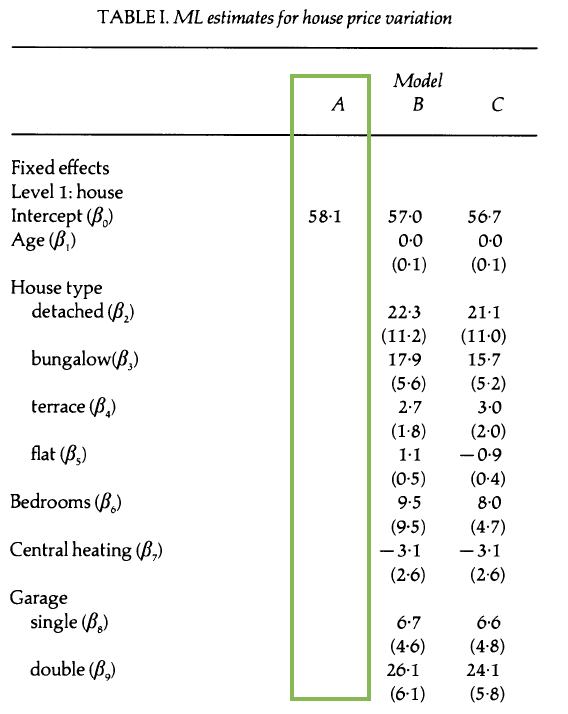
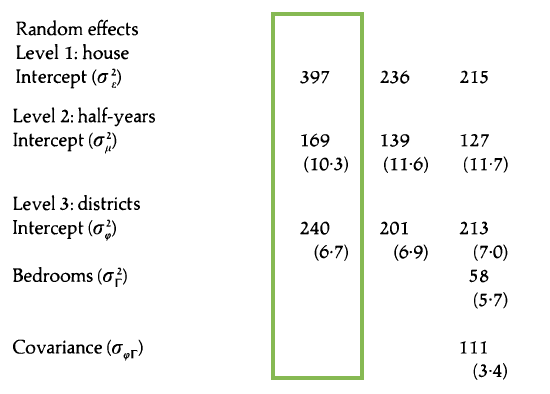
Interpret \(\hat{\beta}_0\) (this is \(\alpha_0\) in our model notation)

Model A: Random effects

  1. Calculate the intraclass correlation for time.
  2. Calculate the intraclass correlation coefficient for districts.
  3. Is there evidence the multilevel model structure is useful for this data?

Model B: Covariates + random intercepts

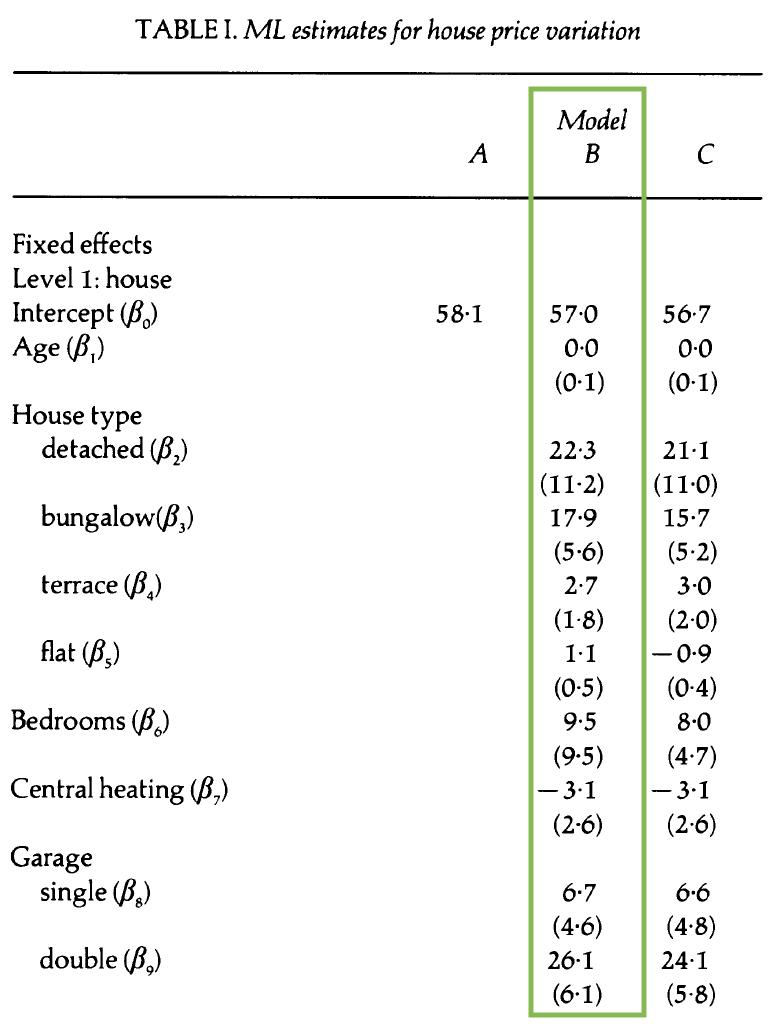
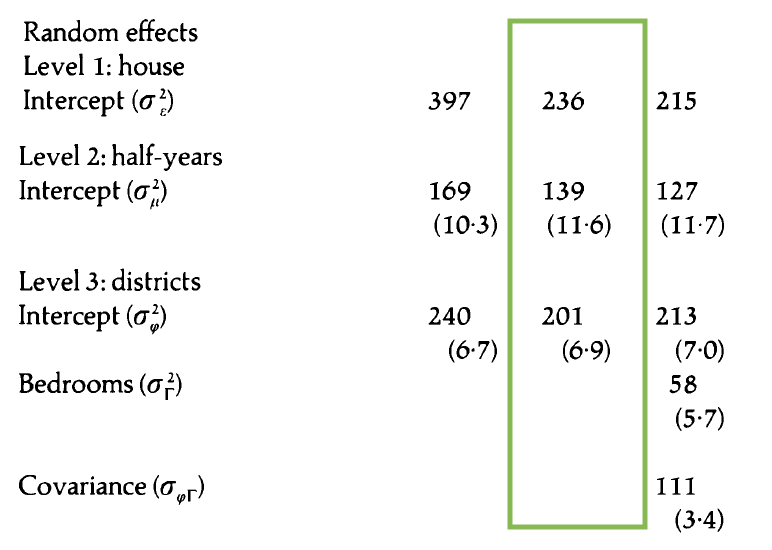
  1. Write the composite model.
  2. Which variables appear to have a statistically significant effect on price?
  3. Use this model to interpret the effect of a double garage on the price of houses in Southampton.

Model C: Additional random effect

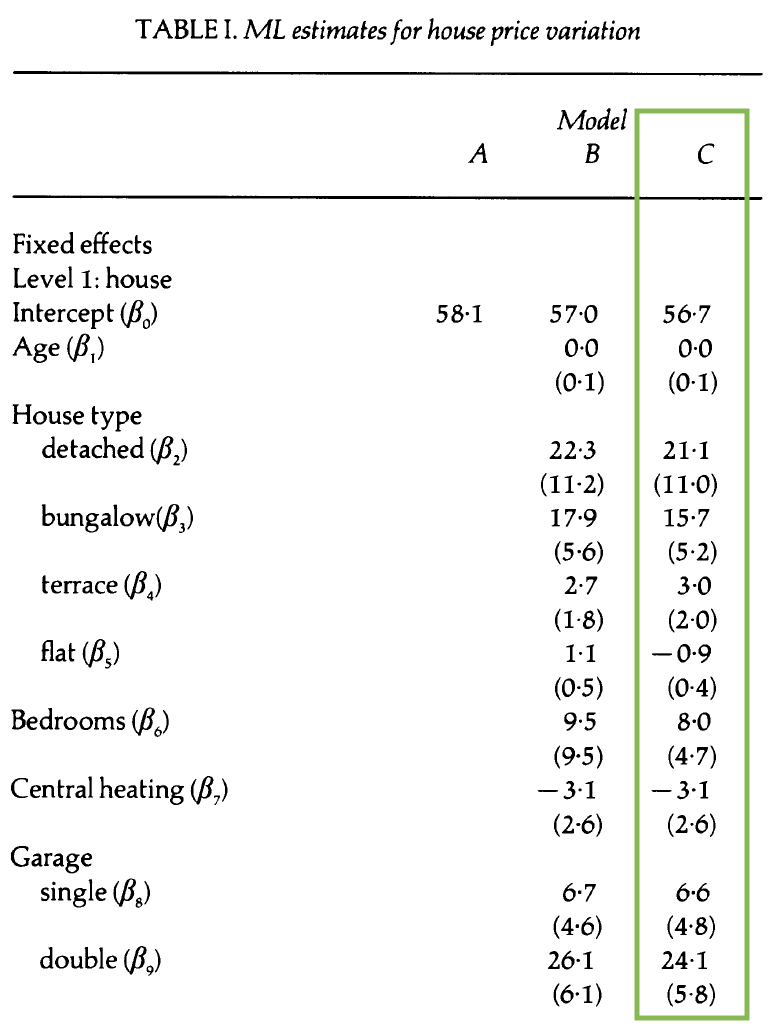
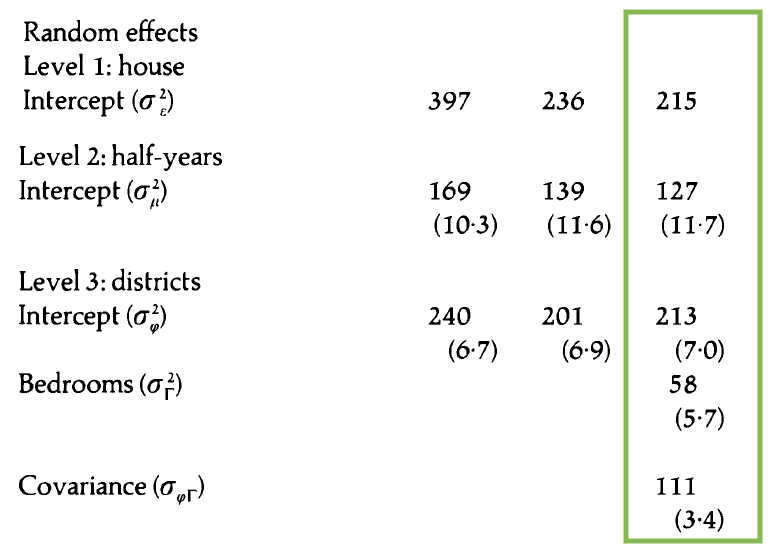
  1. How does this model differ from Model B?
  2. Write the composite model.
  3. Write the Level One, Level Two, and Level Three models.

Visualizing price by district over time

Figure 3 from Jones (1991)
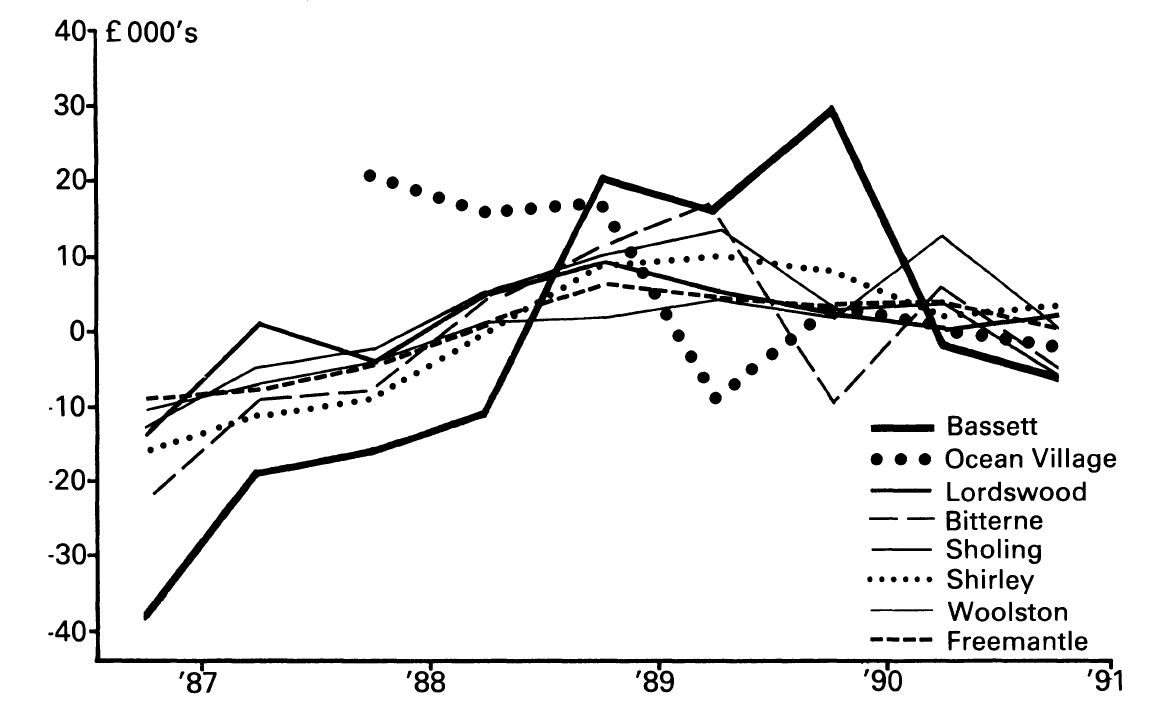
  1. What do you observe from the plot?
  2. What terms in the model can be understood from the plot?
  3. How might you use this type of plot to support decisions you make in the analysis?

Price by district and bedrooms

Figure 4 from Jones (1991)
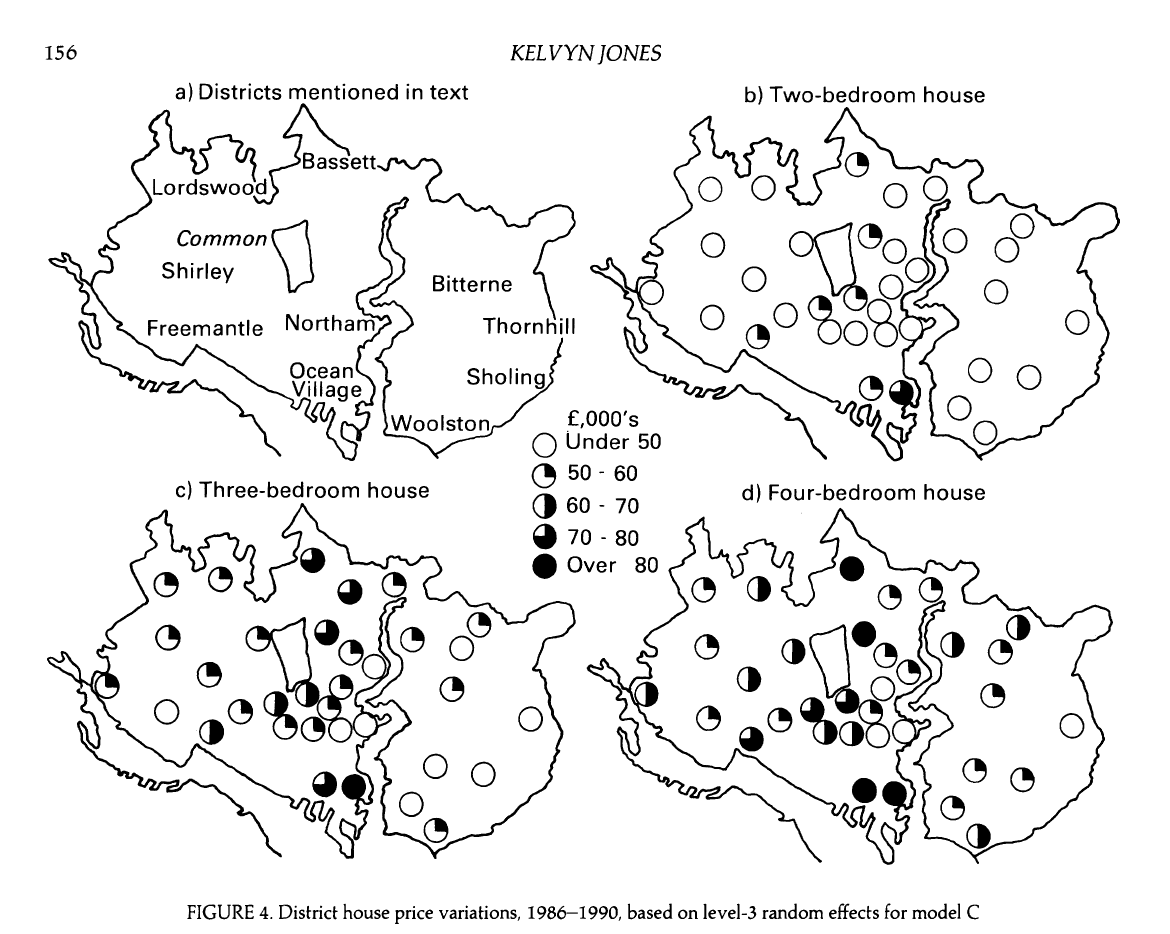
  1. What do you observe from the plot?
  2. What terms in the model can be understood from the plot?
  3. How might you use this type of plot to support decisions you make in the analysis?


How does our understanding of the effect of bedrooms differ in this model compared to Model B?

References

🔗 STA 310 - Spring 2024

Jones, Kelvyn. 1991. “Specifying and Estimating Multi-Level Models for Geographical Research.” Transactions of the Institute of British Geographers, 148–59.
Roback, Paul, and Julie Legler. 2021. Beyond multiple linear regression: applied generalized linear models and multilevel models in R. CRC Press.