Modeling two-level longitudinal data

Inference for fixed and random effects

Prof. Maria Tackett

Mar 06, 2024

Announcements

  • Quiz 03 - due Thu, Mar 07 at noon

    • Covers readings and lectures in Feb 19 - 28 lectures

    • Correlated data, multilevel models

  • HW 04 - due Wed, Mar 20

    • Released Thu, Mar 07 ~ 9am

Topics

  • Inference for fixed and random effects

Modeling two-level longitudinal data

Data: Charter schools in MN

Today’s data set contains standardized test scores and demographic information for schools in Minneapolis, MN from 2008 to 2010. The data were collected by the Minnesota Department of Education. Understanding the effectiveness of charter schools is of particular interest, since they often incorporate unique methods of instruction and learning that differ from public schools.

  • MathAvgScore: Average MCA-II score for all 6th grade students in a school (response variable)
  • urban: urban (1) or rural (0) location school location
  • charter: charter school (1) or a non-charter public school (0)
  • schPctfree: proportion of students who receive free or reduced lunches in a school (based on 2010 figures).
  • year08: Years since 2008

Data

schoolName year08 urban charter schPctfree MathAvgScore
RIPPLESIDE ELEMENTARY 0 0 0 0.363 652.8
RIPPLESIDE ELEMENTARY 1 0 0 0.363 656.6
RIPPLESIDE ELEMENTARY 2 0 0 0.363 652.6
RICHARD ALLEN MATH&SCIENCE ACADEMY 0 1 1 0.545 NA
RICHARD ALLEN MATH&SCIENCE ACADEMY 1 1 1 0.545 NA
RICHARD ALLEN MATH&SCIENCE ACADEMY 2 1 1 0.545 631.2

Closer look at missing data pattern

MathAvgScore0_miss MathAvgScore1_miss MathAvgScore2_miss n
0 0 0 540
0 0 1 6
0 1 0 4
0 1 1 7
1 0 0 25
1 0 1 1
1 1 0 35

Exploratory data analysis

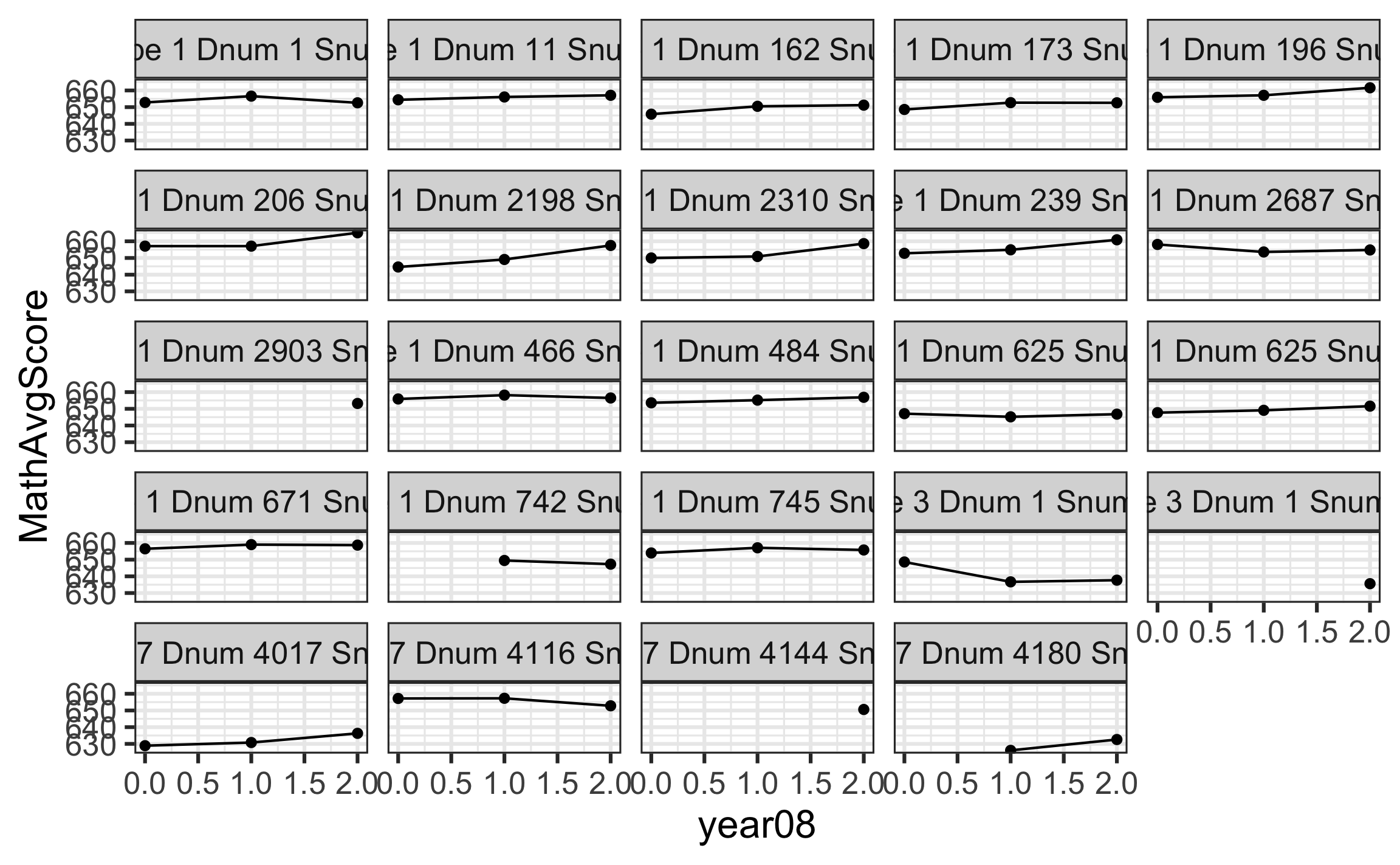
Exploratory data analysis

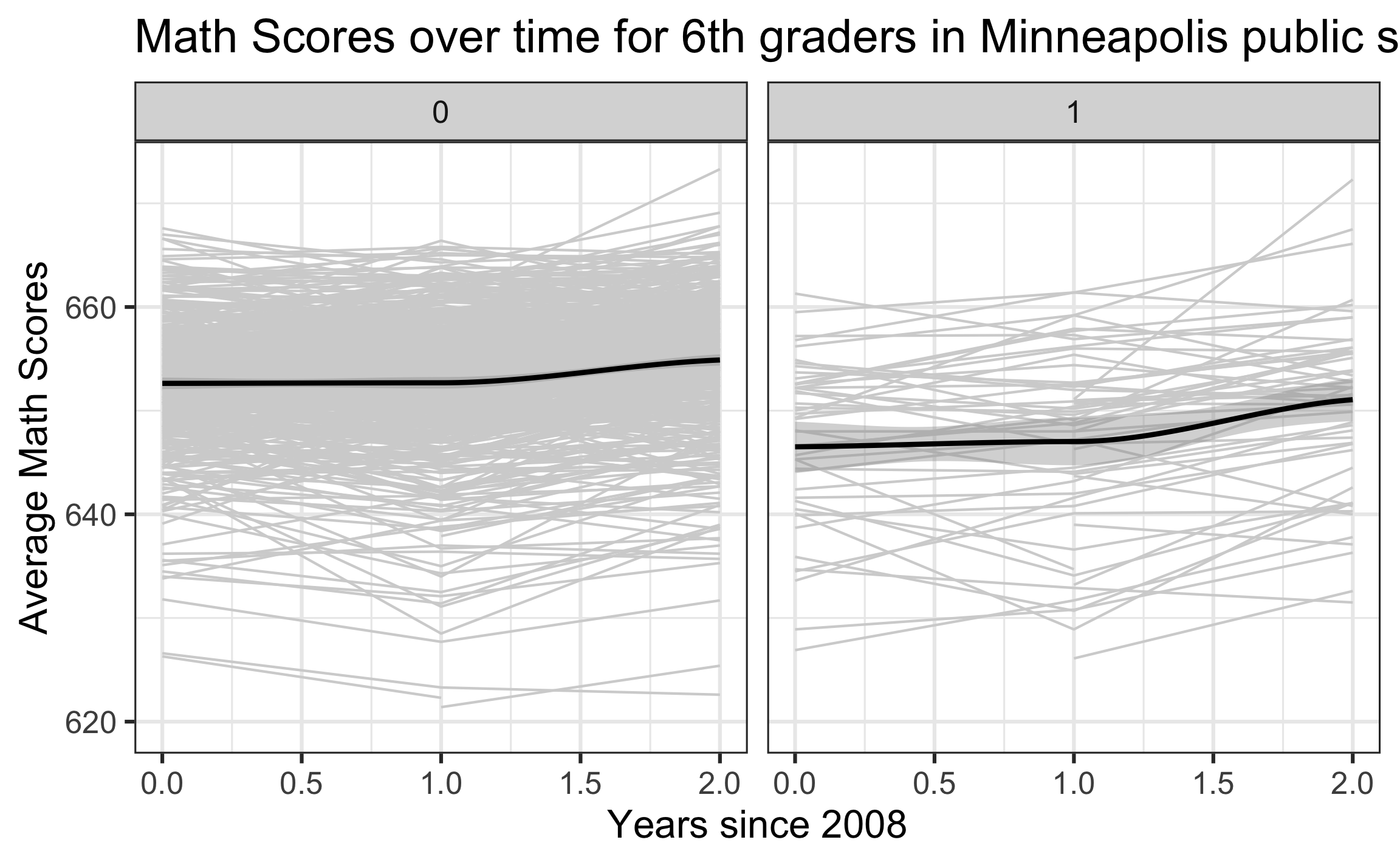
Unconditional means model

Start with the unconditional means model, a model with no covariates at any level. This is also called the random intercepts model.

Level One : \(Y_{ij} = a_{i} + \epsilon_{ij}, \hspace{5mm} \epsilon_{ij} \sim N(0, \sigma^2)\)

Level Two: \(a_i = \alpha_0 + u_i, \hspace{5mm} u_{i} \sim N(0, \sigma^2_u)\)

Unconditional growth model

A next step in the model building is the unconditional growth model, a model with Level One predictors but no Level Two predictors.

Level One

\[ Y_{ij} = a_i + b_iYear08_{ij} + \epsilon_{ij}, \hspace{8mm} \epsilon_{ij} \sim N(0, \sigma^2) \]

Level Two:

\[ \begin{aligned} &a_i = \alpha_0 + u_i \hspace{20mm} b_i = \beta_0 + v_i \\ &\left[ \begin{array}{c} u_{i} \\ v_{i} \end{array} \right] \sim N \left( \left[ \begin{array}{c} 0 \\ 0 \end{array} \right], \left[ \begin{array}{cc} \sigma_{u}^{2} & \sigma_{uv} \\ \sigma_{uv} & \sigma_{v}^{2} \end{array} \right] \right) \end{aligned} \]

Pseudo \(R^2\)

We can use Pseudo R2 to explain changes in variance components between two models

Note: This should only be used when the definition of the variance component is the same between the two models

\[\text{Pseudo }R^2 = \frac{\hat{\sigma}^2(\text{Model 1}) - \hat{\sigma}^2(\text{Model 2})}{\hat{\sigma}^2(\text{Model 1})}\]

We found that 17% of within-school variability in test scores by a change in scores over time.

Model with school-level covariates

Fit a model with school-level covariates that takes the following form:

Level One

\[\begin{equation*} Y_{ij}= a_{i} + b_{i}Year08_{ij} + \epsilon_{ij} \hspace{10mm} \epsilon_{ij} \sim N(0, \sigma^2) \end{equation*}\]

Level Two

\[\begin{align*} a_{i} & = \alpha_{0} + \alpha_{1}charter_i + \alpha_{2}urban_i + \alpha_{3}schpctfree_i + u_{i} \\ b_{i} & = \beta_{0} + \beta_{1}charter_i + \beta_{2}urban_i + v_{i} \\[10pt] &\left[ \begin{array}{c} u_{i} \\ v_{i} \end{array} \right] \sim N \left( \left[ \begin{array}{c} 0 \\ 0 \end{array} \right], \left[ \begin{array}{cc} \sigma_{u}^{2} & \sigma_{uv} \\ \sigma_{uv} & \sigma_{v}^{2} \end{array} \right] \right) \end{align*}\]

Model with school-level covariates

  • Fit the model in R.
  • Use the model to describe how the average math scores differed between charter and non-charter schools.

Consider a simpler model

Would a model without the effects \(v_i\) and \(\rho_{uv}\) be preferable?

Level One

\[\begin{equation*} Y_{ij}= a_{i} + b_{i}Year08_{ij} + \epsilon_{ij} \hspace{10mm} \epsilon_{ij} \sim N(0, \sigma^2) \end{equation*}\]

Level Two

\[\begin{align*} a_{i} & = \alpha_{0} + \alpha_{1}charter_i + \alpha_{2}urban_i + \alpha_{3}schpctfree_i + u_{i} \hspace{10mm} u_i \sim N(0, \sigma_u^2) \\[8pt] b_{i} & = \beta_{0} + \beta_{1}charter_i + \beta_{2}urban_i \end{align*}\]

In this model, the effect of year is the same for all schools with a given combination of charter and urban

Full and reduced models

full_model <- lmer(MathAvgScore ~ charter + urban + schPctfree + 
                     charter:year08  + urban:year08 + year08 + 
                     (year08|schoolid), REML = F, data = charter) 


reduced_model <-  lmer(MathAvgScore ~ charter + urban + schPctfree + 
                     charter:year08  + urban:year08 + year08 +
                       (1 | schoolid), REML = F, data = charter)

Likelihood ratio test

anova(full_model, reduced_model, test = "LRT") |>
  kable(digits = 3)
npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
reduced_model 9 9952.992 10002.11 -4967.496 9934.992 NA NA NA
full_model 11 9953.793 10013.83 -4965.897 9931.793 3.199 2 0.202

  • \(\chi^2\) test is conservative, i.e., the p-values are larger than they should be, when testing random effects at the boundary ( e.g., \(\sigma_v^2 = 0\)) or those with bounded ranges (e.g., \(\rho_{uv}\) )

  • If you observe small p-values, you can feel relatively certain the tested effects are statistically significant

  • Use bootstrap methods to calculate confidence intervals or obtain more accurate p-values for LRT

Bootstrapping

  • Bootstrapping is from the phrase “pulling oneself up by one’s bootstraps”

  • Accomplishing a difficult task without any outside help

  • Task: conduct inference for model parameters (fixed and random effects) using only the sample data

Parametric bootstrap for LRT

1️⃣ Fit the null (reduced) model to obtain the fixed effects and variance components (parametric part).


2️⃣ Use the estimated fixed effects and variance components to generate a new set of response values with the same sample size and associated covariates for each observation as the original data (bootstrap part).


3️⃣ Fit the full and null models to the newly generated data.


4️⃣ Compute the likelihood test statistic comparing the models from the previous step.


5️⃣ Repeat steps 2 - 4 many times (~ 1000).

Parametric bootstrap for LRT

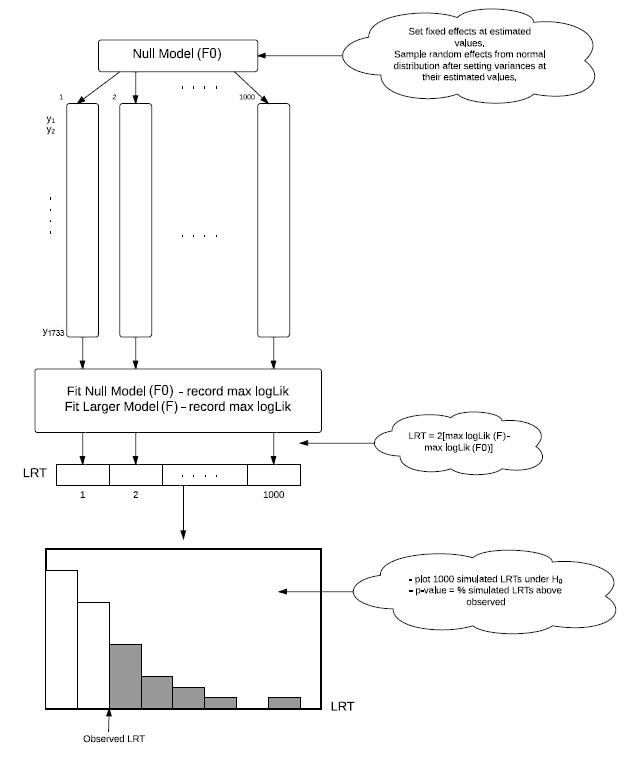
Figure 9.19 in BMLR

Bootstrap CI

Use the confint function to calculate (parametric) bootstrapped confidence intervals to conduct inference on the fixed and random effects

set.seed(310)
confint(full_model, method = "boot", oldNames = FALSE) |>
  kable(digits = 4)
2.5 % 97.5 %
sd_(Intercept)|schoolid 4.0127 4.7203
cor_year08.(Intercept)|schoolid -0.2755 1.0000
sd_year08|schoolid 0.0384 0.9191
sigma 2.7839 3.0873
(Intercept) 659.3502 661.4273
charter1 -4.4390 -1.5448
urban1 -2.0170 -0.2651
schPctfree -19.3348 -16.0699
year08 1.2239 1.8147
charter1:year08 0.4337 1.6641
urban1:year08 -0.9597 -0.1922

Bootstrap CI

2.5 % 97.5 %
sd_(Intercept)|schoolid 4.0127 4.7203
cor_year08.(Intercept)|schoolid -0.2755 1.0000
sd_year08|schoolid 0.0384 0.9191
sigma 2.7839 3.0873
(Intercept) 659.3502 661.4273
charter1 -4.4390 -1.5448
urban1 -2.0170 -0.2651
schPctfree -19.3348 -16.0699
year08 1.2239 1.8147
charter1:year08 0.4337 1.6641
urban1:year08 -0.9597 -0.1922

Would you keep \(\sigma_{v}\) or \(\rho_{uv}\) in the model?

Inference for fixed effects

  • The output for multilevel models do not contain p-values for the coefficients of fixed effects

  • The exact distribution of the test statistic under the null hypothesis (no fixed effect) is unknown, because the exact degrees of freedom are unknown

    • Finding suitable approximations is an area of ongoing research

  • We can use likelihood ratio test with an approximate \(\chi^2\) distribution to test fixed effects

    • Some research suggests the p-values are too low but approximations are generally pretty good
    • Can also calculate the p-values using parametric bootstrap approach (can be computationally intensive)

Methods to conduct inference for individual estimates

  • Use the t-value \(\big(\frac{estimate}{std.error}\big)\) in the model output for fixed effects
    • General rule: Coefficients with |t-value| > 2 considered to be statistically significant, i.e., different from 0
  • Likelihood ratio tests for fixed effects
  • Calculate confidence intervals using parametric bootstrapping for fixed effects and variance components

Summary: Model comparisons

Methods to compare models with different fixed effects

  • AIC or BIC
  • Parametric bootstrap confidence intervals
  • Likelihood ratio tests based on \(\chi^2\) distribution
  • Likelihood ratio test based on parametric bootstrapped p-values (see Section 9.6.4 for more detail)

Methods to compare models with different variance components

  • AIC or BIC
  • Parametric bootstrap confidence intervals
  • Likelihood ratio test based on parametric bootstrapped p-values (see Section 9.6.4 for more detail)

References

🔗 STA 310 - Spring 2024

Boedeker, Peter. 2019. “Hierarchical Linear Modeling with Maximum Likelihood, Restricted Maximum Likelihood, and Fully Bayesian Estimation.” Practical Assessment, Research, and Evaluation 22 (1): 2.
Faraway, Julian J. 2016. Extending the Linear Model with r: Generalized Linear, Mixed Effects and Nonparametric Regression Models. CRC press.
Roback, Paul, and Julie Legler. 2021. Beyond multiple linear regression: applied generalized linear models and multilevel models in R. CRC Press.
Singer, Judith D, and John B Willett. 2003. Applied Longitudinal Data Analysis: Modeling Change and Event Occurrence. Oxford university press.