Multilevel models

Variance components + model fitting

Prof. Maria Tackett

Feb 26, 2024

Announcements

  • HW 03 released tomorrow due Wed, Feb 28 at 11:59pm

    • See Slack for tips from Hun

Topics

  • Write multilevel model, including assumptions about variance components

    • In by-level and composite forms

  • Fit and interpret multilevel models

Data: Music performance anxiety

Today’s data come from the study by Sadler and Miller (2010) of the emotional state of musicians before performances. The data set contains information collected from 37 undergraduate music majors who completed the Positive Affect Negative Affect Schedule (PANAS), an instrument produces a measure of anxiety (negative affect) and a measure of happiness (positive affect). This analysis will focus on negative affect as a measure of performance anxiety.

The primary variables we’ll use are

  • id: unique musician identification number
  • na: negative affect score on PANAS (the response variable)
  • perform_type: type of performance (Solo, Large Ensemble, Small Ensemble)
  • instrument: type of instrument (Voice, Orchestral, Piano)

Look at data

id diary large_ensemble mpqnem orchestra
1 1 0 16 0
1 2 1 16 0
1 3 1 16 0
43 1 0 17 0
43 2 0 17 0
43 3 0 17 0
  • What are the Level One and Level Two observational units?
  • What variables are measured at each level?

Fitting the model

Questions we want to answer

What is the association between performance type (large ensemble or not) and performance anxiety? Does the association differ based on instrument type (orchestral or not)?

Initial modeling approach

Step 1. Fit a separate model for each musician understand the association between performance type (Level One models) and anxiety.


Step 2 . fit a system of Level Two models to predict the fitted coefficients in the Level One model for each subject based on instrument type (Level Two model).

Level One model

We’ll start with the Level One model to understand the association between performance type and performance anxiety for the \(i^{th}\) musician and the \(j^{th}\) performance \[na_{ij} = a_i + b_i ~ LargeEnsemble_{ij} + \epsilon_{ij}, \hspace{5mm} \epsilon_{ij} \sim N(0,\sigma^2)\]


For now, estimate \(a_i\) and \(b_i\) using least-squares regression.

Example Level One model

Below is data for id #22

# A tibble: 15 × 5
      id diary perform_type   instrument               na
   <dbl> <dbl> <chr>          <chr>                 <dbl>
 1    22     1 Solo           orchestral instrument    24
 2    22     2 Large Ensemble orchestral instrument    21
 3    22     3 Large Ensemble orchestral instrument    14
 4    22     4 Large Ensemble orchestral instrument    15
 5    22     5 Large Ensemble orchestral instrument    10
 6    22     6 Solo           orchestral instrument    24
 7    22     7 Solo           orchestral instrument    24
 8    22     8 Solo           orchestral instrument    16
 9    22     9 Small Ensemble orchestral instrument    34
10    22    10 Large Ensemble orchestral instrument    22
11    22    11 Large Ensemble orchestral instrument    19
12    22    12 Large Ensemble orchestral instrument    18
13    22    13 Large Ensemble orchestral instrument    12
14    22    14 Large Ensemble orchestral instrument    19
15    22    15 Solo           orchestral instrument    25

Level One model

music |>
  filter(id == 22) |>
  lm(na ~ large_ensemble, data = _) |>
  tidy() |>
  kable(digits = 3)
term estimate std.error statistic p.value
(Intercept) 24.500 1.96 12.503 0.000
large_ensemble1 -7.833 2.53 -3.097 0.009


Repeat for all 37 musicians.

Level One models

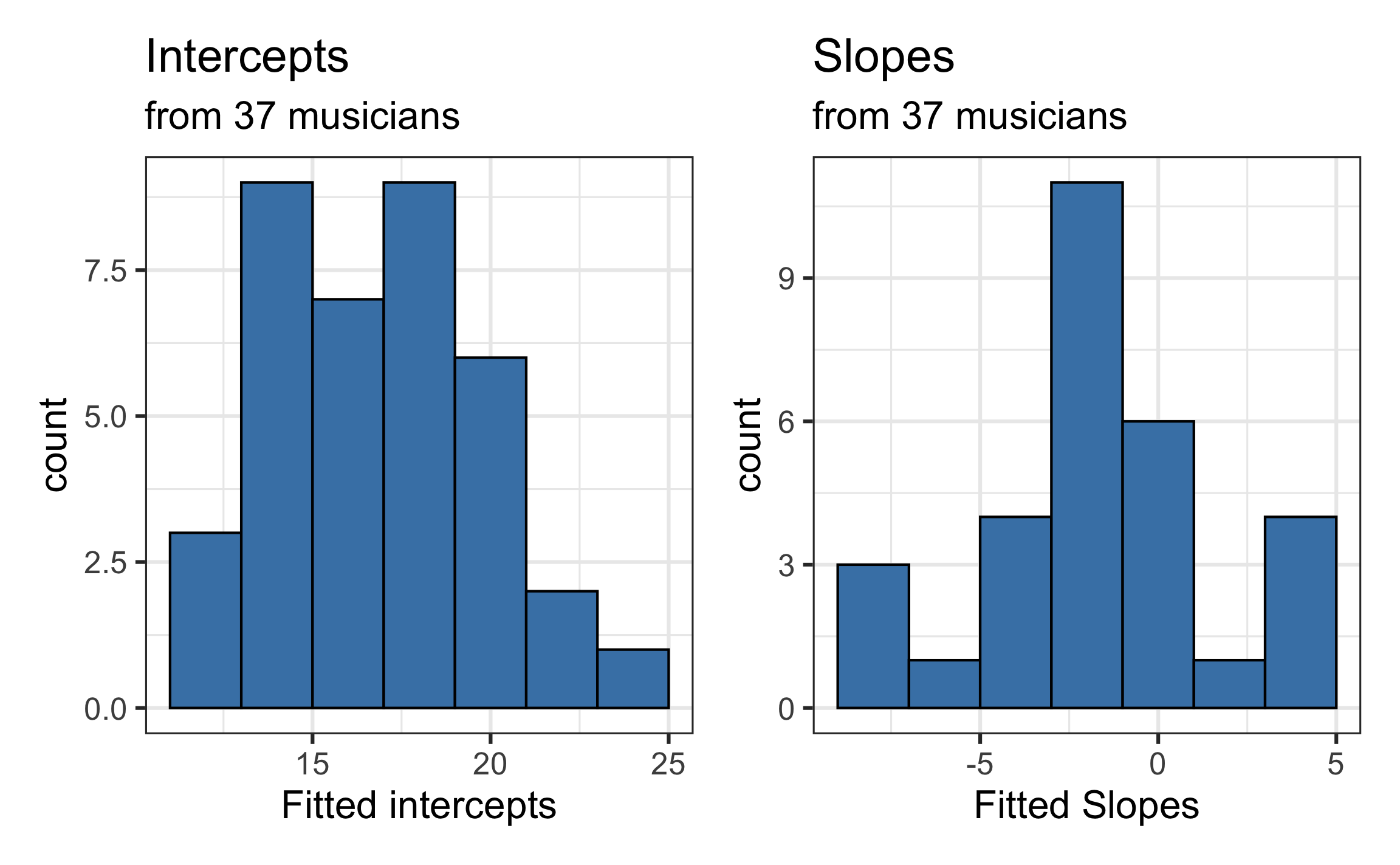
Recreated from BMLR Figure 8.9

Now let’s consider if there is an association between the estimated slopes, estimated intercepts, and the type of instrument

Level Two Model

The slope and intercept for the \(i^{th}\) musician can be modeled as \[\begin{aligned}&a_i = \alpha_0 + \alpha_1 ~ Orchestra_i + u_i \\ &b_i = \beta_0 + \beta_1 ~ Orchestra_i + v_i\end{aligned}\]

Note the response variable in the Level Two models are not observed outcomes but the (fitted) slope and intercept from each musician

Estimated coefficients by instrument

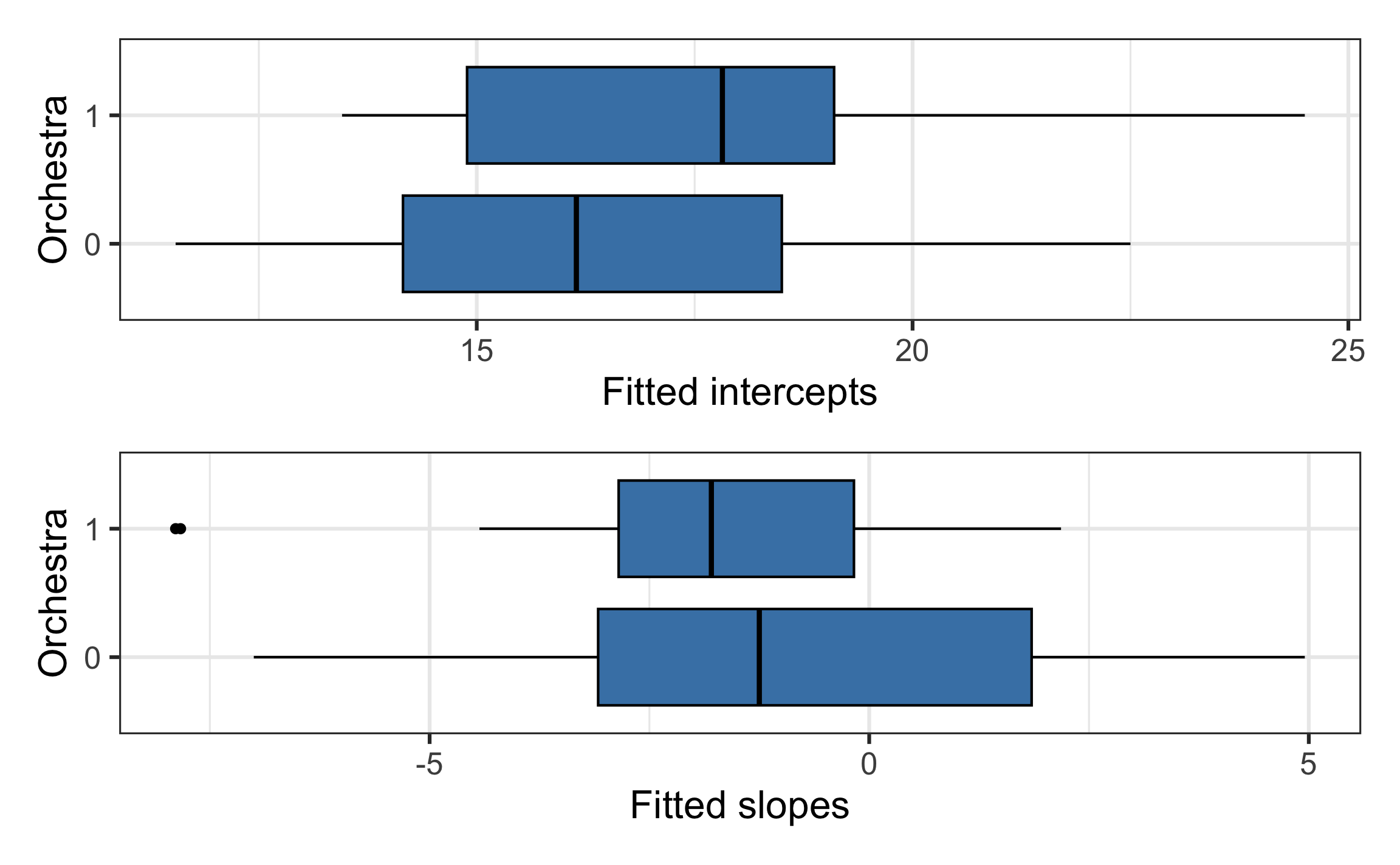
Level Two model

Model for intercepts

term estimate std.error statistic p.value
(Intercept) 16.283 0.671 24.249 0.000
orchestra1 1.411 0.991 1.424 0.163


Model for slopes

term estimate std.error statistic p.value
(Intercept) -0.771 0.851 -0.906 0.373
orchestra1 -1.406 1.203 -1.168 0.253

Estimated two-level model

Level One

\[\hat{na}_{ij} = \hat{a}_i + \hat{b}_i ~ LargeEnsemble_{ij}\]


Level Two

\[\begin{aligned}&\hat{a}_i = 16.283 + 1.411 ~ Orchestra_i \\ &\hat{b}_i = -0.771 - 1.406 ~ Orchestra_i\end{aligned}\]

Estimated composite model

\[ \begin{aligned}\hat{na}_{ij} &= 16.283 + 1.411 ~ Orchestra_i - 0.771 ~ LargeEnsemble_{ij} \\ &- 1.406 ~ Orchestra_i:LargeEnsemble_{ij}\end{aligned} \]

(Note that we also have the error terms \(\epsilon_{ij}, u_i, v_i\) that we will discuss later)

Disadvantages to this approach

⚠️ Weighs each musician the same regardless of number of diary entries

⚠️ Drops subjects who have missing values for slope (7 individuals who didn’t play a large ensemble performance)

⚠️ Does not share strength effectively across individuals


We will use a unified approach that utilizes likelihood-based methods to address some of these drawbacks.

Unified approach to modeling multilevel data

Framework

Let \(Y_{ij}\) be the performance anxiety for the \(i^{th}\) musician before performance \(j\).

Level One

\[Y_{ij} = a_i + b_i ~ LargeEnsemble_{ij} + \epsilon_{ij}\]


Level Two

\[\begin{aligned}&a_i = \alpha_0 + \alpha_1 ~ Orchestra_i+ u_i\\ &b_i = \beta_0 + \beta_1~Orchestra_i + v_i\end{aligned}\]

Note

We will discuss the distribution of the error terms \(\epsilon_{ij}, u_i, v_i\) shortly.

Composite model

Plug in the equations for \(a_i\) and \(b_i\) to get the composite model \[\begin{aligned}Y_{ij} &= (\alpha_0 + \alpha_1 ~ Orchestra_i + \beta_0 ~ LargeEnsemble_{ij} \\ &+ \beta_1 ~ Orchestra_i:LargeEnsemble_{ij})\\ &+ (u_i + v_i ~ LargeEnsemble_{ij} + \epsilon_{ij})\end{aligned}\]

  • The fixed effects to estimate are \(\alpha_0, \alpha_1, \beta_0, \beta_1\)
  • The error terms are \(u_i, v_i, \epsilon_{ij}\)
    • \(u_i\) and \(v_i\) are associated with musician random effect
    • \(\epsilon_{ij}\) is what’s left unexplained

Note that we no longer need to estimate \(a_i\) and \(b_i\) directly as we did earlier. They conceptually connect the Level One and Level Two models.

Notation

  • Greek letters denote the fixed effect model parameters to be estimated

    • e.g., \(\alpha_0, \alpha_1, \beta_0, \beta_1\)

  • Roman letters denote the preliminary fixed effects at lower levels (not directly estimated)

    • e.g. \(a_i, b_i\)

  • \(\sigma\) and \(\rho\) denote variance components that will be estimated

  • \(\epsilon_{ij}, u_i, v_i\) denote error terms (not directly estimated)

Error terms

  • We generally assume that the error terms are normally distributed, e.g. error associated with each performance of a given musician is \(\epsilon_{ij} \sim N(0, \sigma^2)\)
  • For the Level Two models, the errors are
    • \(u_i\): deviation of musician \(i\) from the mean performance anxiety before solos and small ensembles after accounting for the instrument
      • musician-to-musician differences in the intercepts
    • \(v_i\): deviance of musician \(i\) from the mean difference in performance anxiety between large ensembles and other performance types after accounting for instrument
      • musician-to-musician differences in the slopes
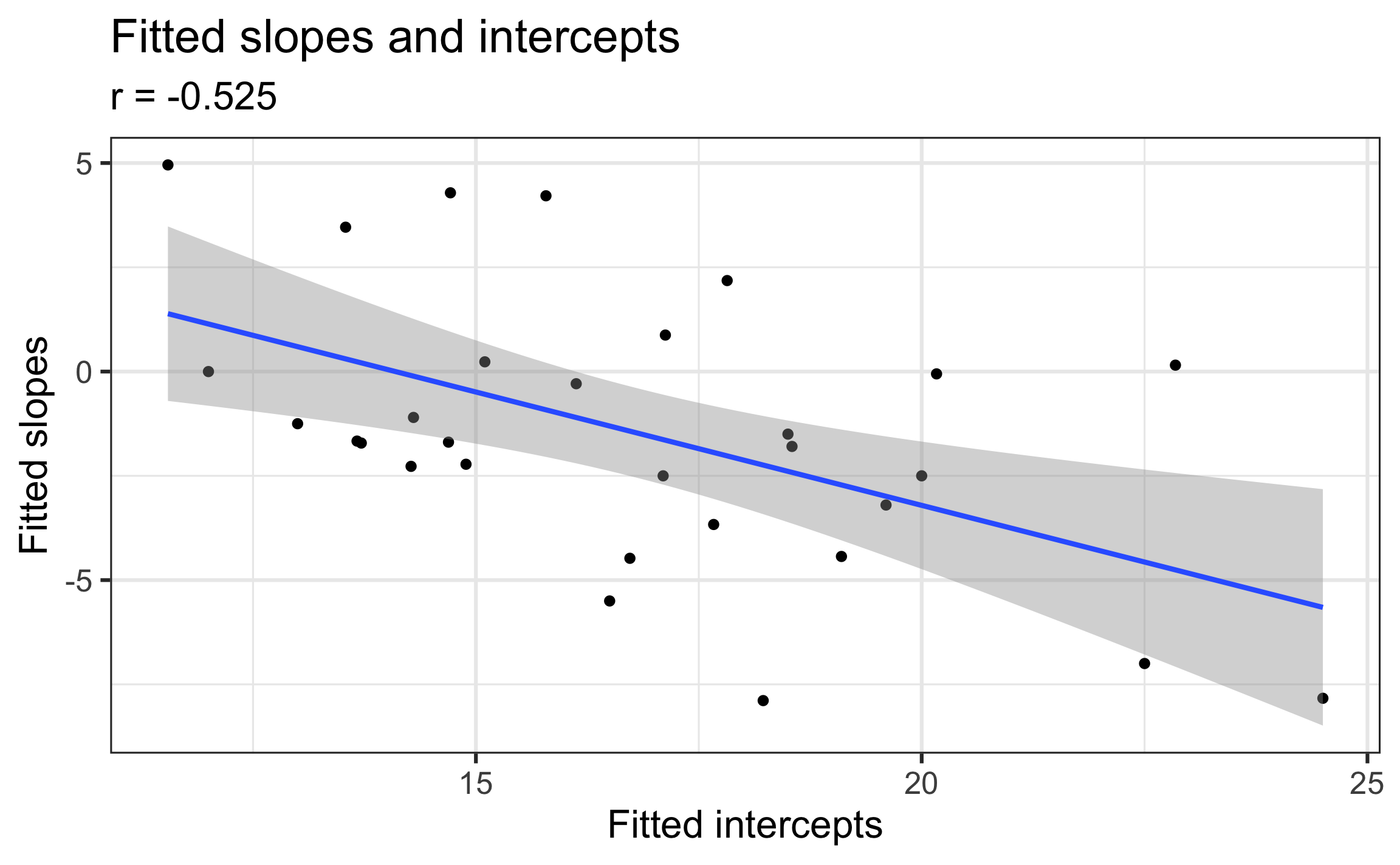
  • Need to account for fact that \(u_i\) and \(v_i\) are correlated for the \(i^{th}\) musician

Recreated from Figure 8.11

Describe what we learn about the association between the slopes and intercepts based on this plot.

Distribution of Level Two errors

Use a multivariate normal distribution for the Level Two error terms \[\left[ \begin{array}{c} u_{i} \\ v_{i} \end{array} \right] \sim N \left( \left[ \begin{array}{c} 0 \\ 0 \end{array} \right], \left[ \begin{array}{cc} \sigma_{u}^{2} & \rho_{uv}\sigma_{u}\sigma_v \\ \rho_{uv}\sigma_{u}\sigma_v & \sigma_{v}^{2} \end{array} \right] \right)\]

where \(\sigma^2_u\) and \(\sigma^2_v\) are the variance of \(u_i\)’s and \(v_i\)’s respectively, and \(\sigma_{uv} = \rho_{uv}\sigma_u\sigma_v\) is covariance between \(u_i\) and \(v_i\)

  • What does it mean for \(\rho_{uv} > 0\)?
  • What does it mean for \(\rho_{uv} < 0\)?

Visualizing multivariate normal distribution

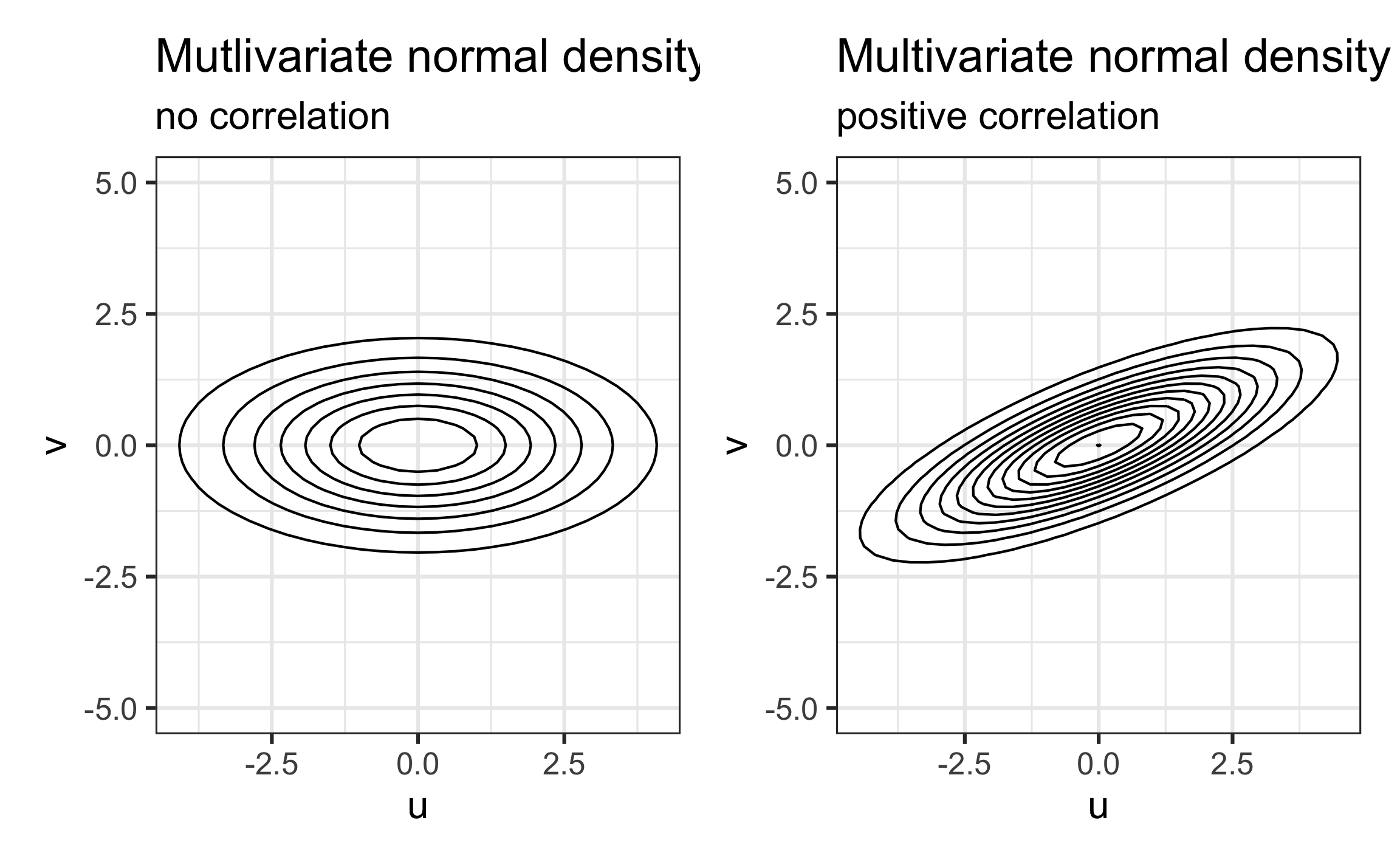
Recreated from Figure 8.12

Fit the model in R

Fit multilevel model using the lmer (“linear mixed effects in R”) function from the lme4 package.

library(lme4)
music_model <- lmer(na ~ orchestra + large_ensemble +
       orchestra:large_ensemble + (large_ensemble|id),
       REML = TRUE, data = music)

  • na ~ orchestra + large_ensemble + orchestra:large_ensemble: Represents the fixed effects

  • (large_ensemble|id): Represents the error terms and associated variance components

    • Specifies two error terms: \(u_i\) corresponding to the intercepts, \(v_i\) corresponding to effect of large ensemble
    • Use (1|id) for models with random intercepts and all other effects fixed.

Tidy output

Display results using the tidy function from the broom.mixed package.

library(broom.mixed)
tidy(music_model)

Get fixed effects only

tidy(music_model) |> filter(effect == "fixed")

Get errors and variance components only

tidy(music_model) |> filter(effect == "ran_pars")

Estimated fixed effects

tidy(music_model) |> 
  filter(effect == "fixed") |> 
  kable(digits = 3)
effect group term estimate std.error statistic
fixed NA (Intercept) 15.930 0.641 24.833
fixed NA orchestra1 1.693 0.945 1.791
fixed NA large_ensemble1 -0.911 0.845 -1.077
fixed NA orchestra1:large_ensemble1 -1.424 1.099 -1.295

Estimated random effects

tidy(music_model) |> 
  filter(effect == "ran_pars") |> 
  kable(digits = 3)
effect group term estimate std.error statistic
ran_pars id sd__(Intercept) 2.378 NA NA
ran_pars id cor__(Intercept).large_ensemble1 -0.635 NA NA
ran_pars id sd__large_ensemble1 0.672 NA NA
ran_pars Residual sd__Observation 4.670 NA NA

Fitted model

\[ \begin{aligned} \hat{na}_{ij} &= 15.930 + 1.693 ~ Orchestra_i - 0.911 ~ LargeEnsemble_{ij} \\ &- 1.424 ~ Orchestra_i:LargeEnsemble_{ij} \\[30pt]&\left[ \begin{array}{c} u_{i} \\ v_{i} \end{array} \right] \sim N \left( \left[ \begin{array}{c} 0 \\ 0 \end{array} \right], \left[ \begin{array}{cc} 2.378^{2} & -0.635 *2.378 *0.672 \\ -0.635 *2.378 *0.672 & 0.672^{2} \end{array} \right] \right) \\[30pt] &\epsilon_{ij} \sim N(0, 4.670^2) \end{aligned} \]

Sadler and Miller (2010)

Read the Data Analysis Section in Sadler and Miller (2010). Click here to access the paper in Canvas. Use the text to answer the following:

  1. What is the goal of the analysis?
  2. What type of model is used? What is the response variable? What is the multilevel structure?
  3. Describe the details of the model estimation.
  4. Describe the data wrangling / creation of new variables. What were the goals of the data wrangling steps?
  5. How as model performance assessed?
06:00

Sadler and Miller 2010

  • Split into 3 - 5 groups and discuss your responses.

  • One person will write your group’s response to your assigned question(s).

  • Click here to access the slides.

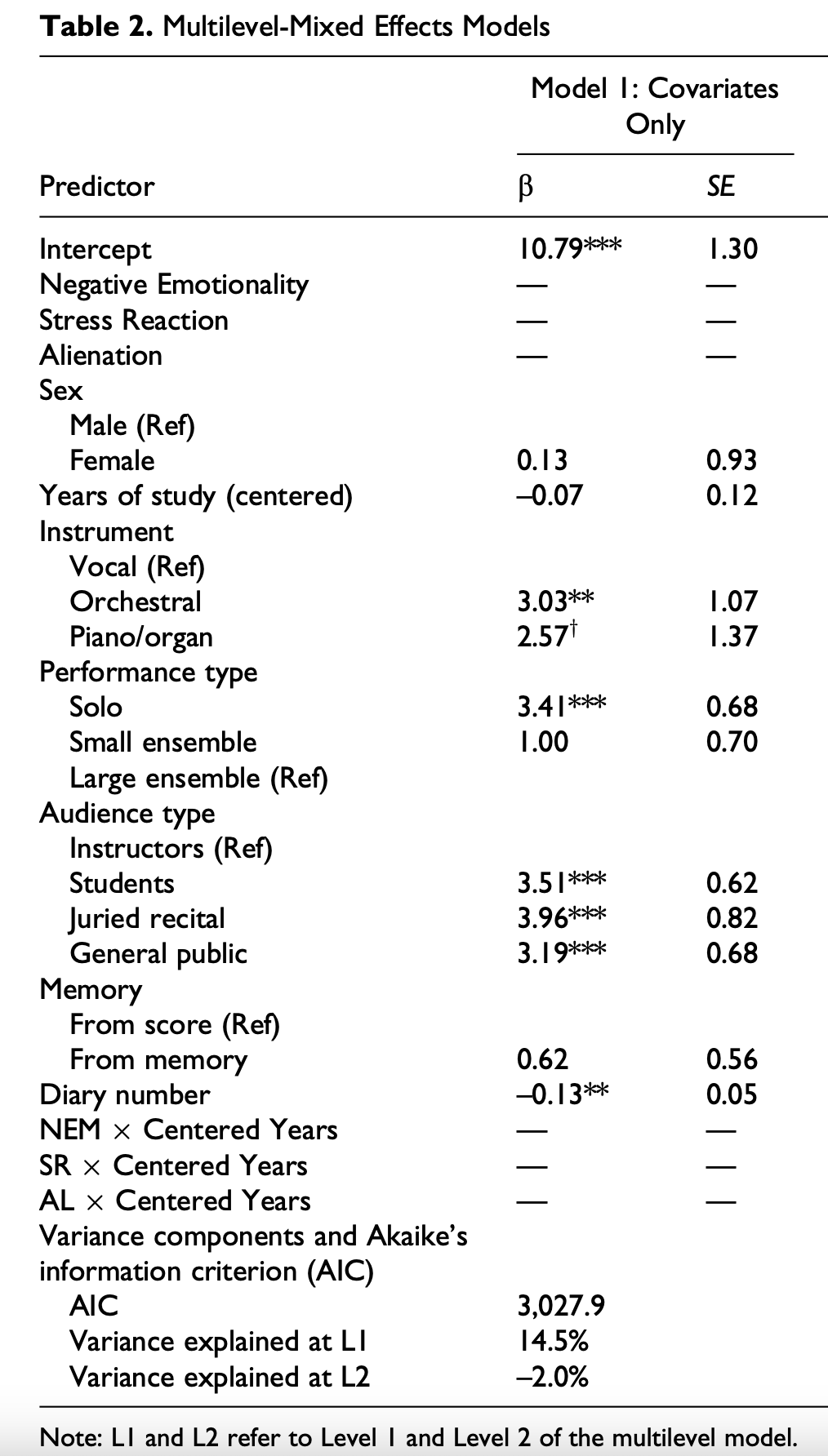
Sadler and Miller (2010) Model 1

References

🔗 STA 310 - Spring 2024

Roback, Paul, and Julie Legler. 2021. Beyond multiple linear regression: applied generalized linear models and multilevel models in R. CRC Press.
Sadler, Michael E, and Christopher J Miller. 2010. “Performance Anxiety: A Longitudinal Study of the Roles of Personality and Experience in Musicians.” Social Psychological and Personality Science 1 (3): 280–87.