Multilevel models

Prof. Maria Tackett

Feb 21, 2024

Announcements

  • Quiz 02: due Thu, Feb 22, 12pm (noon)

    • Covers readings & lectures: Jan 24 - Feb 12

    • Poisson regression, unifying framework for GLMs, logistic regression, proportional odds models, probit regression

  • HW 02 returned

    • Close issue in your GitHub after you’ve reviewed feedback

  • HW 03 released tomorrow and due Wed, Feb 28

  • Read Sadler and Miller (2010) as part of Feb 26 prepare assignment

Topics

  • Understand how multilevel models can be used to take correlation into account

  • Conduct univariate and bivariate EDA for multilevel models

  • Write multilevel model, including assumptions about variance components

    • In by-level and composite forms

  • Interpret the model parameters, fixed effects, and variance components

Correlated observations

Multilevel data

  • We can think of correlated data as a multilevel structure

    • Population elements are aggregated into groups
    • There are observational units and measurements at each level

  • For now we will focus on data with two levels:

    • Level one: Most basic level of observation
    • Level two: Groups formed from aggregated level-one observations

Two types of effects

  • Fixed effects: Effects that are of interest in the study
    • Can think of these as effects whose interpretations would be included in a write up of the study
  • Random effects: Not interested in studying effects of specific values in the data but we want to understand the variability
    • Can think of these as effects whose interpretations would not necessarily be included in a write up of the study

Example

Researchers are interested in understanding the effect social media has on opinions about a proposed economic plan. They randomly select 1000 households. They ask each adult in the household how many minutes they spend on social media daily and whether they support the proposed economic plan.

  • daily minutes on social media is the fixed effect
  • household is the random effect

Multilevel models

Data: Music performance anxiety

Today’s data come from the study by Sadler and Miller (2010) of the emotional state of musicians before performances. The data set contains information collected from 37 undergraduate music majors who completed the Positive Affect Negative Affect Schedule (PANAS), an instrument produces a measure of anxiety (negative affect) and a measure of happiness (positive affect). This analysis will focus on negative affect as a measure of performance anxiety.

The primary variables we’ll use are

  • id: unique musician identification number
  • na: negative affect score on PANAS (the response variable)
  • perform_type: type of performance (Solo, Large Ensemble, Small Ensemble)
  • instrument: type of instrument (Voice, Orchestral, Piano)

Look at data

id diary perform_type na gender instrument
1 1 Solo 11 Female voice
1 2 Large Ensemble 19 Female voice
1 3 Large Ensemble 14 Female voice
12 1 Solo 23 Female orchestral instrument
12 2 Solo 17 Female orchestral instrument
12 3 Small Ensemble 25 Female orchestral instrument
  • What are the Level One and Level Two observational units?
  • What variables are measured at each level?

Univariate exploratory data analysis

Level One variables

Two ways to approach univariate EDA (visualizations and summary statistics) for Level One variables:

  • Use individual observations (i.e., treat observations as independent)

  • Use aggregated values for each Level Two observation

Level Two variables

  • Use a data set that contains one row per Level Two observation

Bivariate exploratory data analysis

Goals

  • Explore general association between the predictor and response variable
  • Explore whether subjects at a given level of the predictor tend to have similar mean responses
  • Explore whether variation in response differs at different levels of a predictor

There are two ways to visualize these associations:

  • One plot of response vs. predictor for individual observations (i.e., treat observations as independent)

  • Separate plots of responses vs. predictor for each Level Two observation (lattice plots)

Application exercise

📋 sta310-sp24.netlify.app/ae/lec-11-multilevel

06:00

Fitting the model

Questions we want to answer

What is the association between performance type (large ensemble or not) and performance anxiety? Does the association differ based on instrument type (orchestral or not)?


What is the problem with an ordinary least squares model to draw conclusions?

term estimate std.error statistic p.value
(Intercept) 15.721 0.359 43.778 0.000
orchestra1 1.789 0.552 3.243 0.001
large_ensemble1 -0.277 0.791 -0.350 0.727
orchestra1:large_ensemble1 -1.709 1.062 -1.609 0.108

Other modeling approaches

1️⃣ Condense each musician’s set of responses into a single outcome (e.g., mean, max, last observation, etc.), and fit a linear model on these condensed observations

  • Leaves only a few observations (37) to fit the model
  • Ignoring a lot of information in the multiple observations for each musician

2️⃣ Fit a separate model for each musician understand the association between performance type (Level One models) and anxiety. Then fit a system of Level Two models to predict the fitted coefficients in the Level One model for each subject based on instrument type (Level Two model).

Let’s look at approach #2

Level One model

We’ll start with the Level One model to understand the association between performance type and performance anxiety for the \(i^{th}\) musician and the \(j^{th}\) performance \[na_{ij} = a_i + b_i ~ LargeEnsemble_{ij} + \epsilon_{ij}, \hspace{5mm} \epsilon_{ij} \sim N(0,\sigma^2)\]


Why is it more meaningful to use performance type for the Level One model than instrument?

For now, estimate \(a_i\) and \(b_i\) using least-squares regression.

Example Level One model

Below is data for id #22

# A tibble: 15 × 5
      id diary perform_type   instrument               na
   <dbl> <dbl> <chr>          <chr>                 <dbl>
 1    22     1 Solo           orchestral instrument    24
 2    22     2 Large Ensemble orchestral instrument    21
 3    22     3 Large Ensemble orchestral instrument    14
 4    22     4 Large Ensemble orchestral instrument    15
 5    22     5 Large Ensemble orchestral instrument    10
 6    22     6 Solo           orchestral instrument    24
 7    22     7 Solo           orchestral instrument    24
 8    22     8 Solo           orchestral instrument    16
 9    22     9 Small Ensemble orchestral instrument    34
10    22    10 Large Ensemble orchestral instrument    22
11    22    11 Large Ensemble orchestral instrument    19
12    22    12 Large Ensemble orchestral instrument    18
13    22    13 Large Ensemble orchestral instrument    12
14    22    14 Large Ensemble orchestral instrument    19
15    22    15 Solo           orchestral instrument    25

Level One model

music |>
  filter(id == 22) |>
  lm(na ~ large_ensemble, data = _) |>
  tidy() |>
  kable(digits = 3)
term estimate std.error statistic p.value
(Intercept) 24.500 1.96 12.503 0.000
large_ensemble1 -7.833 2.53 -3.097 0.009


Repeat for all 37 musicians. See Part 3: Level One Models in AE.

Level One models

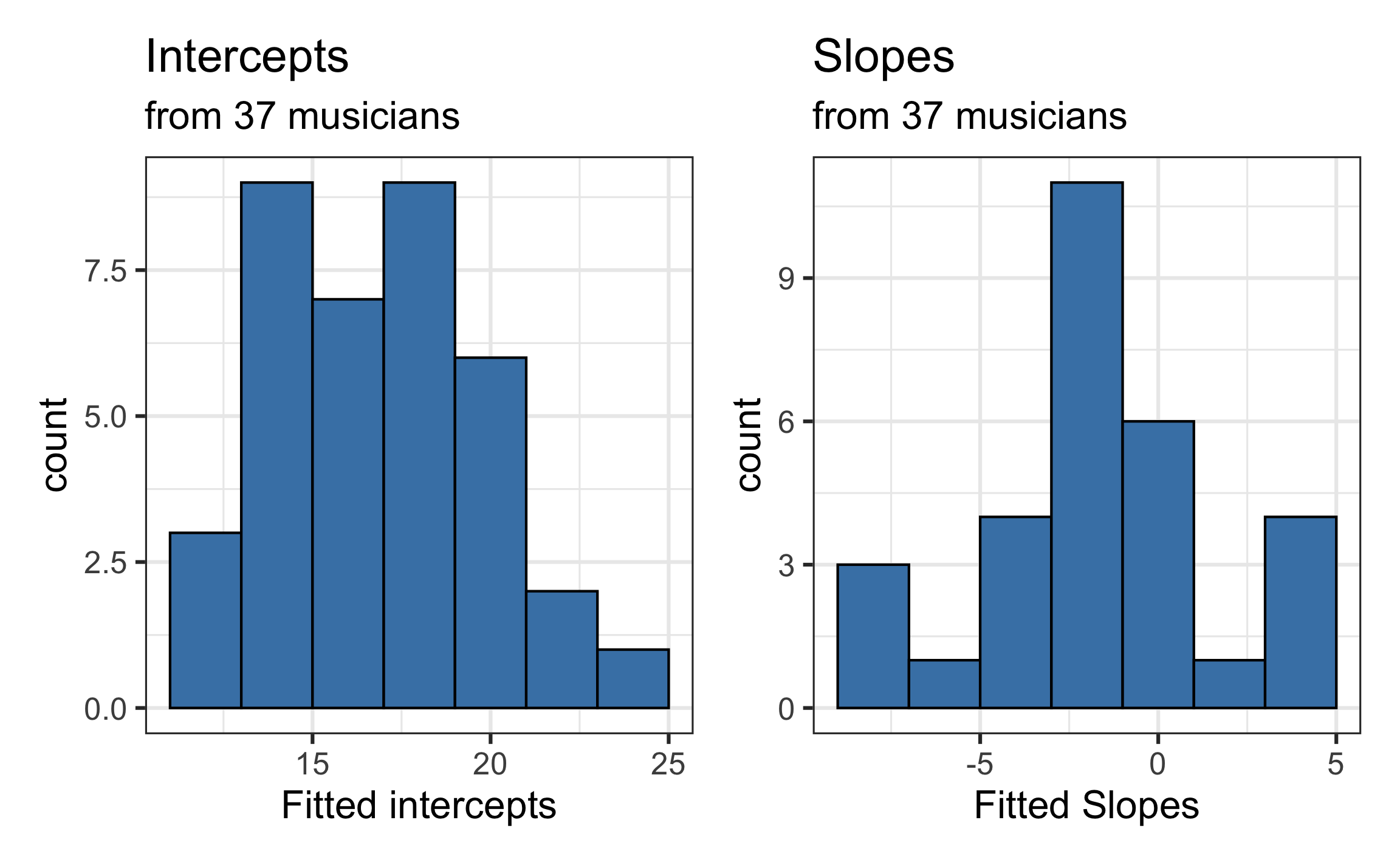
Recreated from BMLR Figure 8.9

Now let’s consider if there is an association between the estimated slopes, estimated intercepts, and the type of instrument

Level Two Model

The slope and intercept for the \(i^{th}\) musician can be modeled as \[\begin{aligned}&a_i = \alpha_0 + \alpha_1 ~ Orchestra_i + u_i \\ &b_i = \beta_0 + \beta_1 ~ Orchestra_i + v_i\end{aligned}\]

Note the response variable in the Level Two models are not observed outcomes but the (fitted) slope and intercept from each musician

See Part 4: Level Two Models in AE.

Estimated coefficients by instrument

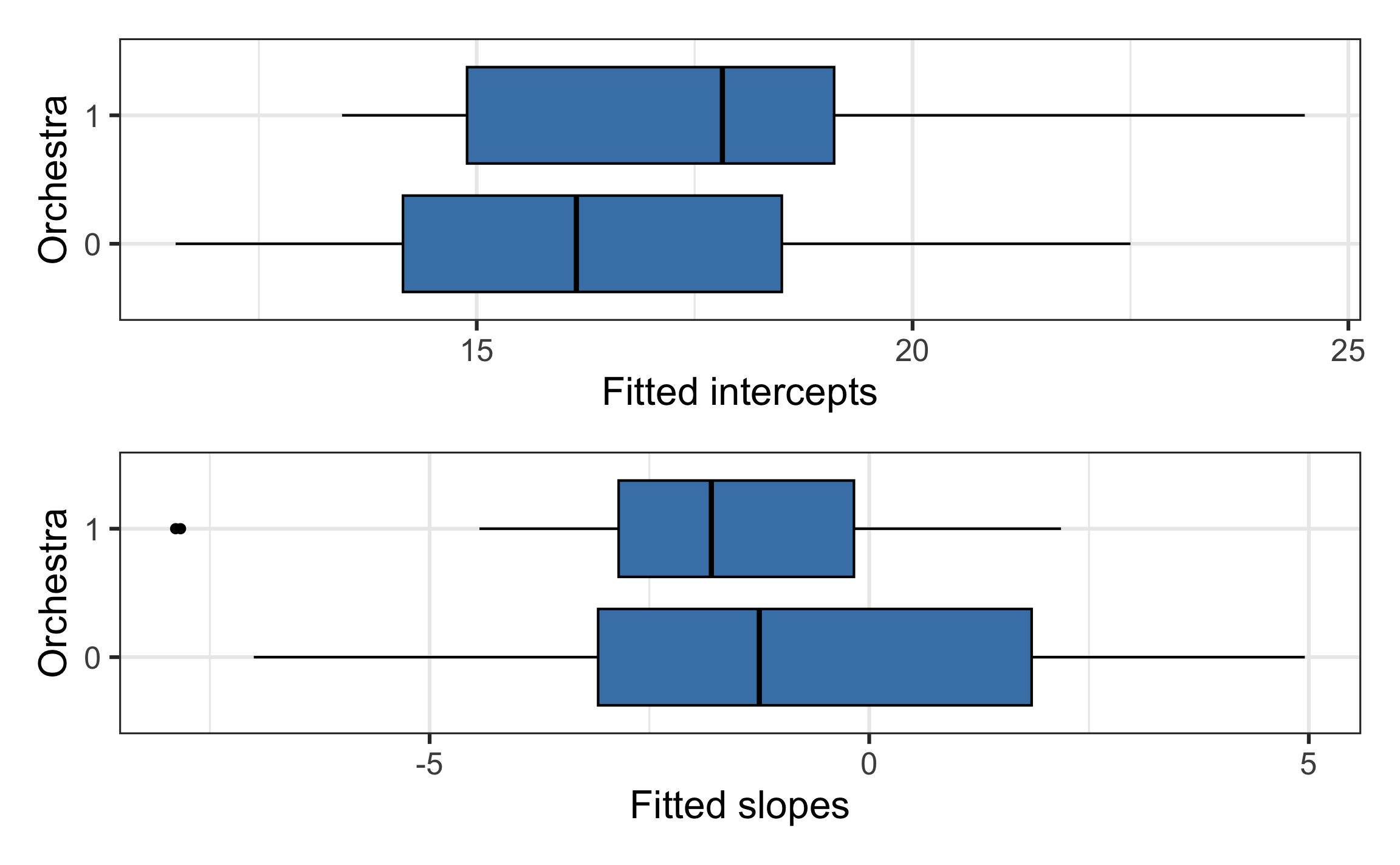
Level Two model

Model for intercepts

term estimate std.error statistic p.value
(Intercept) 16.283 0.671 24.249 0.000
orchestra1 1.411 0.991 1.424 0.163


Model for slopes

term estimate std.error statistic p.value
(Intercept) -0.771 0.851 -0.906 0.373
orchestra1 -1.406 1.203 -1.168 0.253

Writing out the models

Level One

\[\hat{na}_{ij} = \hat{a}_i + \hat{b}_i ~ LargeEnsemble_{ij}\]


Level Two

\[\begin{aligned}&\hat{a}_i = 16.283 + 1.411 ~ Orchestra_i \\ &\hat{b}_i = -0.771 - 1.406 ~ Orchestra_i\end{aligned}\]

Estimated composite model

\[ \begin{aligned}\hat{na}_{ij} &= 16.283 + 1.411 ~ Orchestra_i - 0.771 ~ LargeEnsemble_{ij} \\ &- 1.406 ~ Orchestra_i:LargeEnsemble_{ij}\end{aligned} \]

(Note that we also have the error terms \(\epsilon_{ij}, u_i, v_i\) that we will discuss later)


  1. What is the predicted average performance anxiety before solos and small ensemble performances for vocalists and keyboardists? For those who play orchestral instruments?

  2. What is the predicted average performance anxiety before large ensemble performances for those who play orchestral instruments?

Disadvantages to this approach

⚠️ Weighs each musician the same regardless of number of diary entries

⚠️ Drops subjects who have missing values for slope (7 individuals who didn’t play a large ensemble performance)

⚠️ Does not share strength effectively across individuals (look at \(R^2\) values in Part 3: Level One Models of AE)


We will use a unified approach that utilizes likelihood-based methods to address some of these drawbacks.

Unified approach to modeling multilevel data

Framework

Let \(Y_{ij}\) be the performance anxiety for the \(i^{th}\) musician before performance \(j\).

Level One

\[Y_{ij} = a_i + b_i ~ LargeEnsemble_{ij} + \epsilon_{ij}\]


Level Two

\[\begin{aligned}&a_i = \alpha_0 + \alpha_1 ~ Orchestra_i+ u_i\\ &b_i = \beta_0 + \beta_1~Orchestra_i + v_i\end{aligned}\]

Note

We will discuss the distribution of the error terms \(\epsilon_{ij}, u_i, v_i\) shortly.

Composite model

Plug in the equations for \(a_i\) and \(b_i\) to get the composite model \[\begin{aligned}Y_{ij} &= (\alpha_0 + \alpha_1 ~ Orchestra_i + \beta_0 ~ LargeEnsemble_{ij} \\ &+ \beta_1 ~ Orchestra_i:LargeEnsemble_{ij})\\ &+ (u_i + v_i ~ LargeEnsemble_{ij} + \epsilon_{ij})\end{aligned}\]

  • The fixed effects to estimate are \(\alpha_0, \alpha_1, \beta_0, \beta_1\)
  • The error terms are \(u_i, v_i, \epsilon_{ij}\)
    • \(u_i\) and \(v_i\) are associated with musician random effect
    • \(\epsilon_{ij}\) is what’s left unexplained

Note that we no longer need to estimate \(a_i\) and \(b_i\) directly as we did earlier. They conceptually connect the Level One and Level Two models.

Notation

  • Greek letters denote the fixed effect model parameters to be estimated

    • e.g., \(\alpha_0, \alpha_1, \beta_0, \beta_1\)

  • Roman letters denote the preliminary fixed effects at lower levels (not directly estimated)

    • e.g. \(a_i, b_i\)

  • \(\sigma\) and \(\rho\) denote variance components that will be estimated

  • \(\epsilon_{ij}, u_i, v_i\) denote error terms (not directly estimated)

Error terms

  • We generally assume that the error terms are normally distributed, e.g. error associated with each performance of a given musician is \(\epsilon_{ij} \sim N(0, \sigma^2)\)
  • For the Level Two models, the errors are
    • \(u_i\): deviation of musician \(i\) from the mean performance anxiety before solos and small ensembles after accounting for the instrument
      • musician-to-musician differences in the intercepts
    • \(v_i\): deviance of musician \(i\) from the mean difference in performance anxiety between large ensembles and other performance types after accounting for instrument
      • musician-to-musician differences in the slopes
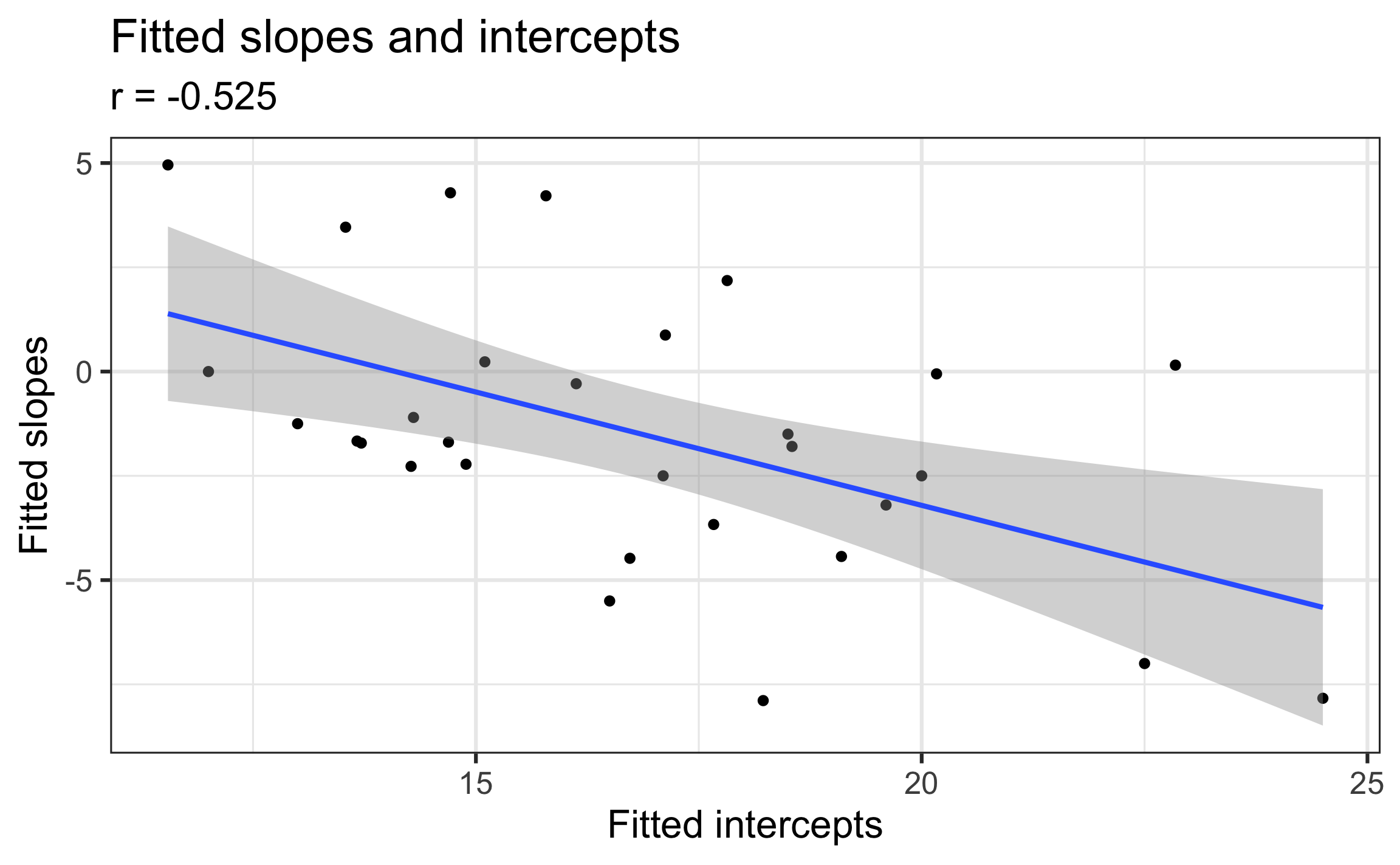
  • Need to account for fact that \(u_i\) and \(v_i\) are correlated for the \(i^{th}\) musician

Recreated from Figure 8.11

Describe what we learn about the association between the slopes and intercepts based on this plot.

Distribution of Level Two errors

Use a multivariate normal distribution for the Level Two error terms \[\left[ \begin{array}{c} u_{i} \\ v_{i} \end{array} \right] \sim N \left( \left[ \begin{array}{c} 0 \\ 0 \end{array} \right], \left[ \begin{array}{cc} \sigma_{u}^{2} & \rho_{uv}\sigma_{u}\sigma_v \\ \rho_{uv}\sigma_{u}\sigma_v & \sigma_{v}^{2} \end{array} \right] \right)\]

where \(\sigma^2_u\) and \(\sigma^2_v\) are the variance of \(u_i\)’s and \(v_i\)’s respectively, and \(\sigma_{uv} = \rho_{uv}\sigma_u\sigma_v\) is covariance between \(u_i\) and \(v_i\)

  • What does it mean for \(\rho_{uv} > 0\)?
  • What does it mean for \(\rho_{uv} < 0\)?

Visualizing multivariate normal distribution

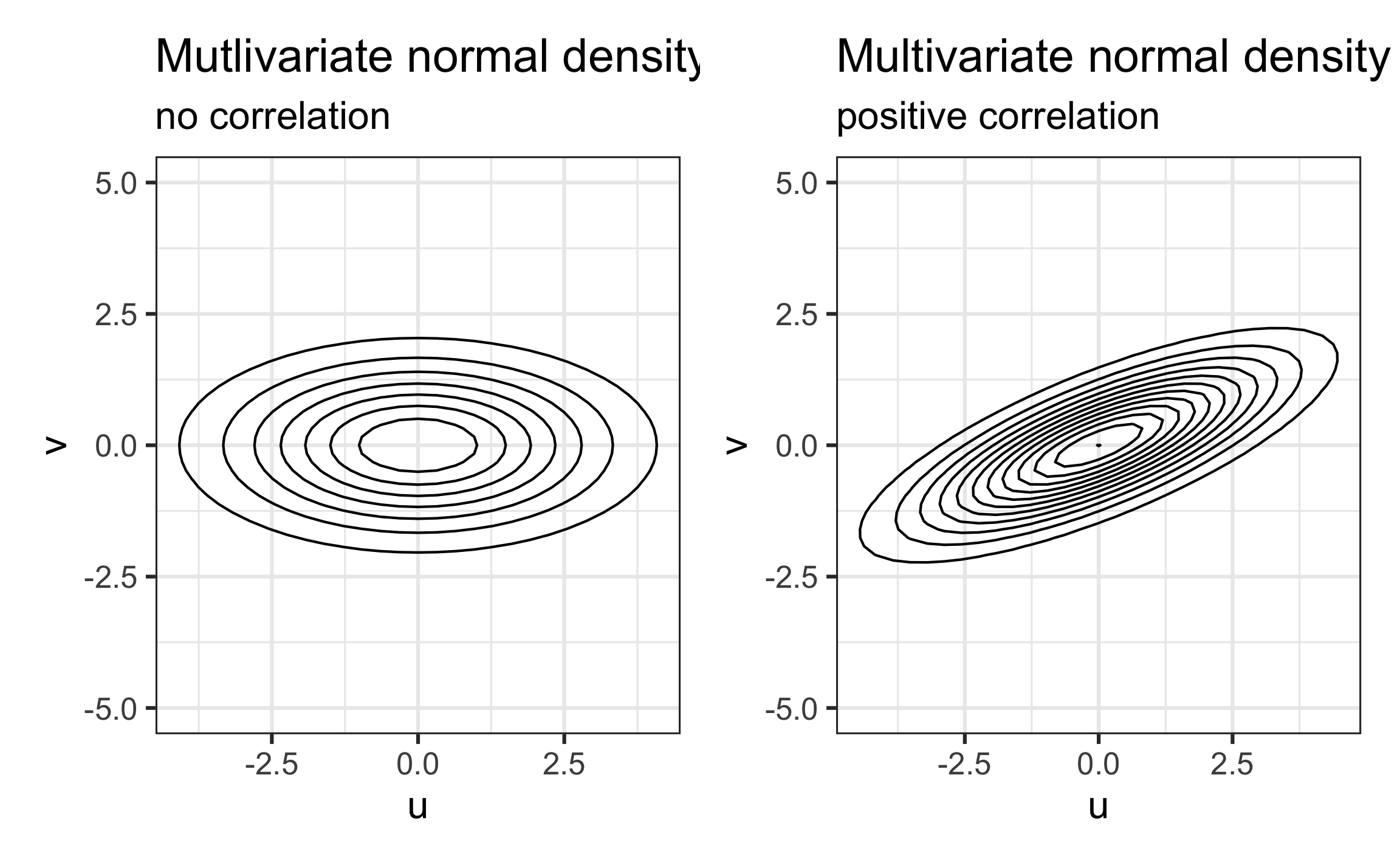
Recreated from Figure 8.12

Fit the model

Fit multilevel model using the lmer function from the lme4 package. Display results using the tidy() function from the broom.mixed package.


library(lme4)
library(broom.mixed)

music_model <- lmer(na ~ orchestra + large_ensemble + 
                      orchestra:large_ensemble +
                      (large_ensemble|id), 
                    REML = TRUE, data = music)

tidy(music_model) |> kable(digits = 3)

Fitted model

effect group term estimate std.error statistic
fixed NA (Intercept) 15.930 0.641 24.833
fixed NA orchestra1 1.693 0.945 1.791
fixed NA large_ensemble1 -0.911 0.845 -1.077
fixed NA orchestra1:large_ensemble1 -1.424 1.099 -1.295
ran_pars id sd__(Intercept) 2.378 NA NA
ran_pars id cor__(Intercept).large_ensemble1 -0.635 NA NA
ran_pars id sd__large_ensemble1 0.672 NA NA
ran_pars Residual sd__Observation 4.670 NA NA

Fitted model

\[ \begin{aligned} \hat{na}_{ij} &= 15.930 + 1.693 ~ Orchestra_i - 0.911 ~ LargeEnsemble_{ij} \\ &- 1.424 ~ Orchestra_i:LargeEnsemble_{ij} \\[30pt]&\left[ \begin{array}{c} u_{i} \\ v_{i} \end{array} \right] \sim N \left( \left[ \begin{array}{c} 0 \\ 0 \end{array} \right], \left[ \begin{array}{cc} 2.378^{2} & -0.635 *2.378 *0.672 \\ -0.635 *2.378 *0.672 & 0.672^{2} \end{array} \right] \right) \\[30pt] &\epsilon_{ij} \sim N(0, 4.670^2) \end{aligned} \]

References

🔗 STA 310 - Spring 2024

Roback, Paul, and Julie Legler. 2021. Beyond multiple linear regression: applied generalized linear models and multilevel models in R. CRC Press.
Sadler, Michael E, and Christopher J Miller. 2010. “Performance Anxiety: A Longitudinal Study of the Roles of Personality and Experience in Musicians.” Social Psychological and Personality Science 1 (3): 280–87.