Logistic regression

Prof. Maria Tackett

Feb 05, 2024

Topics

• Identify Bernoulli and binomial random variables

• Write GLM for binomial response variable

• Interpret the coefficients for a logistic regression model

Notes based on Chapter 6 Roback and Legler (2021) unless noted otherwise.

Basics of logistic regression

Bernoulli + Binomial random variables

Logistic regression is used to analyze data with two types of responses:

• Binary: These responses take on two values success \((Y = 1)\) or failure \((Y = 0)\), yes \((Y = 1)\) or no \((Y = 0)\), etc.

\[P(Y = y) = p^y(1-p)^{1-y} \hspace{10mm} y = 0, 1\]

• Binomial: Number of successes in a Bernoulli process, \(n\) independent trials with a constant probability of success \(p\).

\[P(Y = y) = {n \choose y}p^{y}(1-p)^{n - y} \hspace{10mm} y = 0, 1, \ldots, n\]

In both instances, the goal is to model \(p\) the probability of success.

Binary vs. Binomial data

For each example, identify if the response is a Bernoulli or Binomial response:

1. Use median age and unemployment rate in a county to predict the percent of Obama votes in the county in the 2008 presidential election.
2. Use GPA and MCAT scores to estimate the probability a student is accepted into medical school.
3. Use sex, age, and smoking history to estimate the probability an individual has lung cancer.
4. Use offensive and defensive statistics from the 2017-2018 NBA season to predict a team’s winning percentage.

03:00

Logistic regression model

\[ \log\Big(\frac{p}{1-p}\Big) = \beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_px_p \]

• The response variable, \(\log\Big(\frac{p}{1-p}\Big)\), is the log(odds) of success, i.e. the logit

• Use the model to calculate the probability of success \[\hat{p} = \frac{e^{\beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_px_p}}{1 + e^{\beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_px_p}}\]

• When the response is a Bernoulli random variable, the probabilities can be used to classify each observation as a success or failure

Logistic vs linear regression model

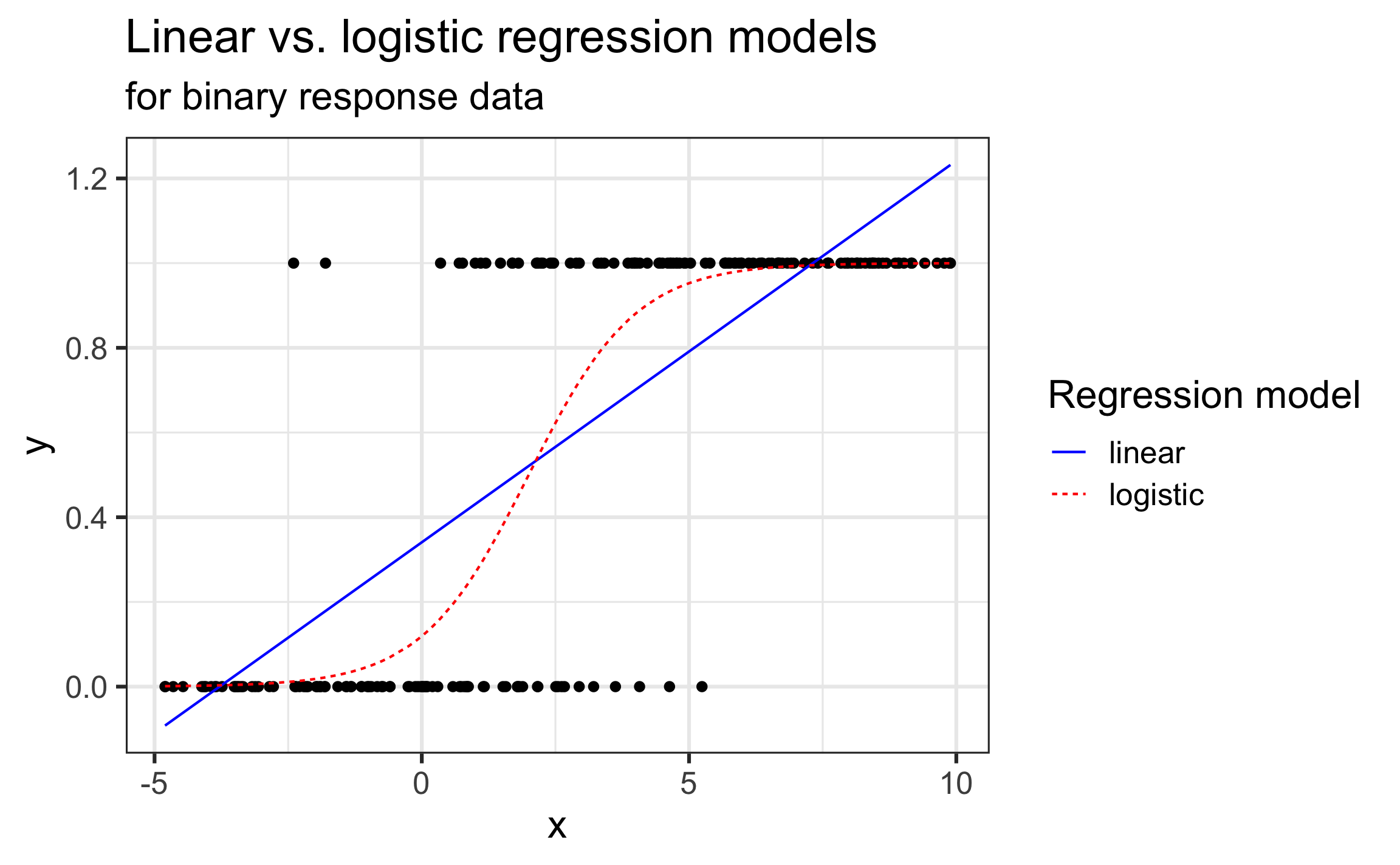
Graph from BMLR Chapter 6

Logit link

Bernoulli and Binomial random variables can be written in one-parameter exponential family form, \(f(y;\theta) = e^{[a(y)b(\theta) + c(\theta) + d(y)]}\)

Bernoulli

\[f(y;p) = e^{y\log(\frac{p}{1-p}) + \log(1-p)}\]

Binomial

\[f(y;n,p) = e^{y\log(\frac{p}{1-p}) + n\log(1-p) + \log{n \choose y}}\]

They have the same canonical link \(b(p) = \log\big(\frac{p}{1-p}\big)\)

Assumptions for logistic regression

The following assumptions need to be satisfied to use logistic regression to make inferences

1️⃣ \(\hspace{0.5mm}\) Binary response: The response is dichotomous (has two possible outcomes) or is the sum of dichotomous responses

2️⃣ \(\hspace{0.5mm}\) Independence: The observations must be independent of one another

3️⃣ \(\hspace{0.5mm}\) Variance structure: Variance of a binomial random variable is \(np(1-p)\) \((n = 1 \text{ for Bernoulli})\) , so the variability is highest when \(p = 0.5\)

4️⃣ \(\hspace{0.5mm}\) Linearity: The log of the odds ratio, \(\log\big(\frac{p}{1-p}\big)\), must be a linear function of the predictors \(x_1, \ldots, x_p\)

COVID-19 infection prevention practices at food establishments

Researchers at Wollo Univeristy in Ethiopia conducted a study in July and August 2020 to understand factors associated with good COVID-19 infection prevention practices at food establishments. Their study is published in Andualem et al. (2022) .

They were particularly interested in the understanding implementation of prevention practices at food establishments, given the workers’ increased risk due to daily contact with customers.

The data

“An institution-based cross-sectional study was conducted among 422 food handlers in Dessie City and Kombolcha Town food and drink establishments in July and August 2020. The study participants were selected using a simple random sampling technique. Data were collected by trained data collectors using a pretested structured questionnaire and an on-the-spot observational checklist.”

Response variable

“The outcome variable of this study was the good or poor practices of COVID-19 infection prevention among food handlers. Nine yes/no questions, one observational checklist and five multiple choice infection prevention practices questions were asked with a minimum score of 1 and maximum score of 25. Good infection prevention practice (the variable of interest) was determined for food handlers who scored 75% or above, whereas poor infection prevention practices refers to those food handlers who scored below 75% on the practice questions.”

Results

Interpreting the results

• Is the response a Bernoulli or Binomial?

• What is the strongest predictor of having good COVID-19 infection prevention practices?

  • It’s often unreliable to look answer this question just based on the model output. Why are we able to answer this question based on the model output in this case?

• Describe the effect (coefficient interpretation and inference) of having COVID-19 infection prevention policies available at the food establishment.

• The intercept describes what group of food handlers?

04:30

References

Andualem, Atsedemariam, Belachew Tegegne, Sewunet Ademe, Tarikuwa Natnael, Gete Berihun, Masresha Abebe, Yeshiwork Alemnew, et al. 2022. “COVID-19 Infection Prevention Practices Among a Sample of Food Handlers of Food and Drink Establishments in Ethiopia.” PLoS One 17 (1): e0259851.

Roback, Paul, and Julie Legler. 2021. Beyond multiple linear regression: applied generalized linear models and multilevel models in R. CRC Press.