STA 310 - Spring 2024 - Poisson Regression

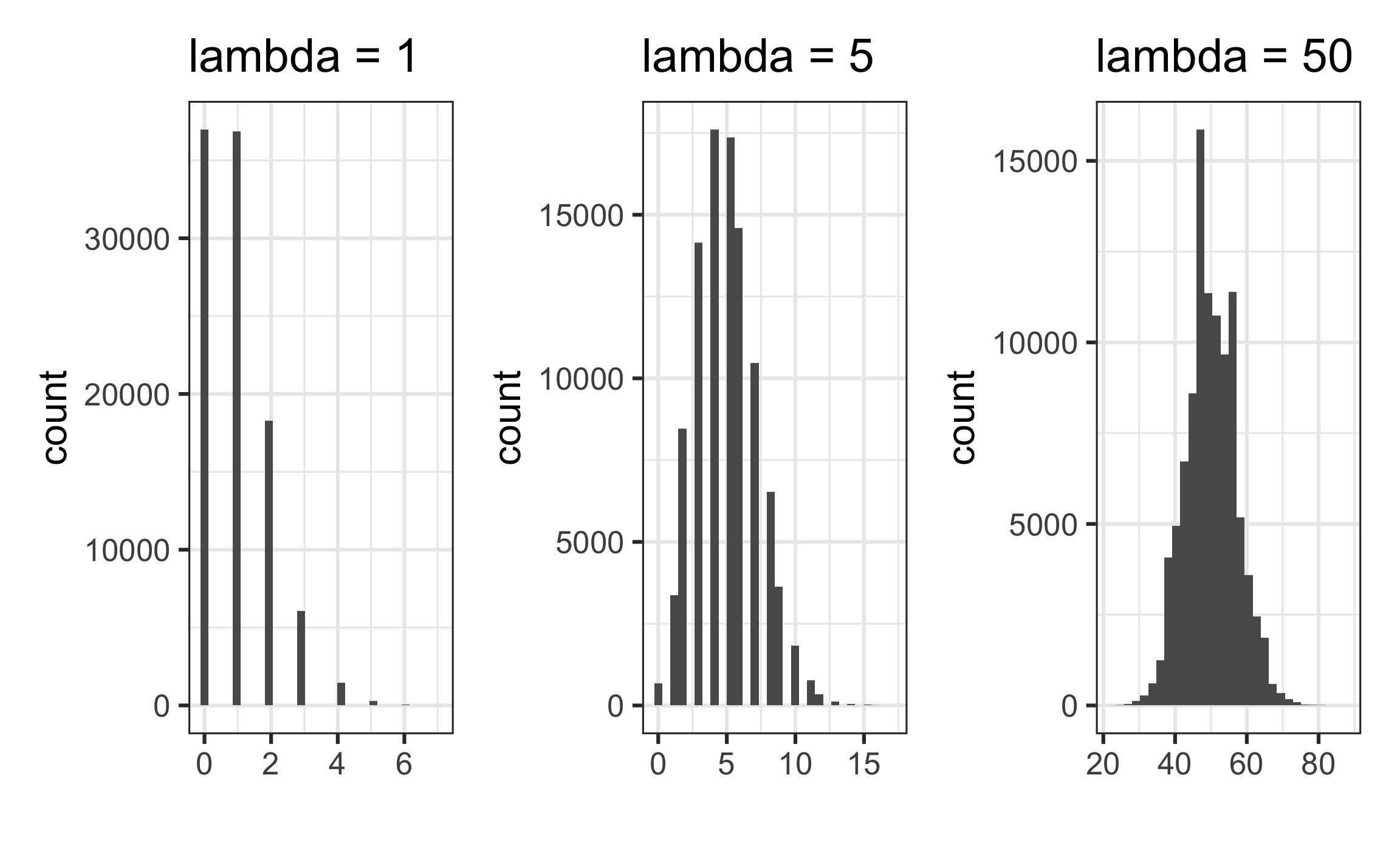
	Mean	Variance
lambda = 1	0.99351	0.9902178
lambda = 5	4.99367	4.9865798
lambda = 50	49.99288	49.8962683

The data: Household size in the Philippines

The data fHH1.csv come from the 2015 Family Income and Expenditure Survey conducted by the Philippine Statistics Authority.

Goal: Understand the association between household size and various characteristics of the household

Response:

total: Number of people in the household other than the head

Predictors:

location: Where the house is located
age: Age of the head of household
roof: Type of roof on the residence (proxy for wealth)

Other variables:

numLT5: Number in the household under 5 years old

The data

hh_data <- read_csv("data/fHH1.csv")
hh_data |> slice(1:5) |> kable()

location	age	total	roof
CentralLuzon	65	0	Predominantly Strong Material
MetroManila	75	3	Predominantly Strong Material
DavaoRegion	54	4	Predominantly Strong Material
Visayas	49	3	Predominantly Strong Material
MetroManila	74	3	Predominantly Strong Material

Response variable

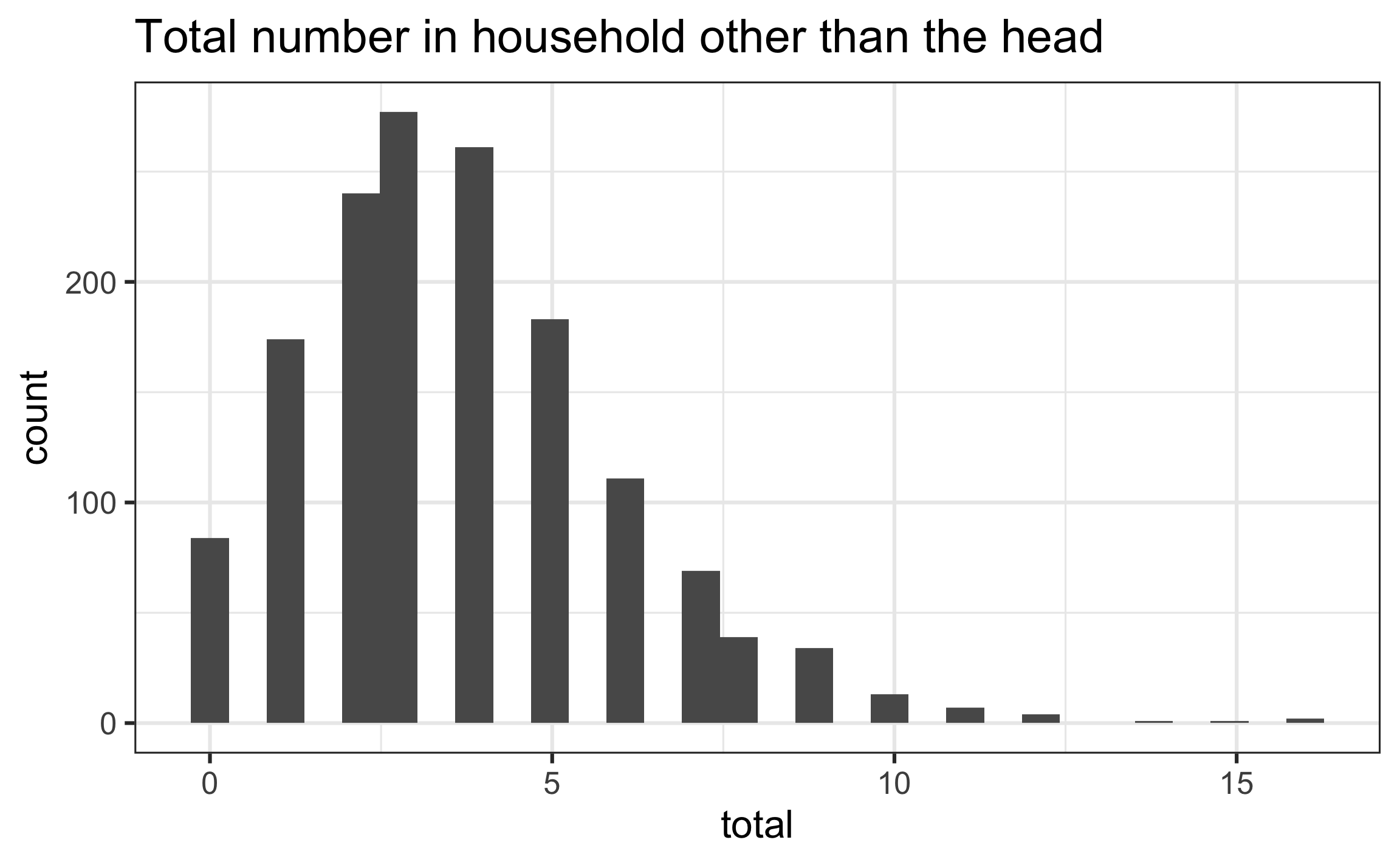
mean	var
3.685	5.534

Why the least-squares model doesn’t work

The goal is to model $λ$ , the expected number of people in the household (other than the head), as a function of the predictors (covariates)

We might be tempted to try a linear model $λ_{i} = β_{0} + β_{1} x_{i 1} + β_{2} x_{i 2} + \dots + β_{p} x_{i p}$

This model won’t work because…

It could produce negative values of $λ$ for certain values of the predictors
The equal variance assumption required to conduct inference for linear regression is violated.

Poisson regression model

If $Y_{i} \sim P o i s s o n$ with $λ = λ_{i}$ for the given values $x_{i 1}, \dots, x_{i p}$ , then

$\log (λ_{i}) = β_{0} + β_{1} x_{i 1} + β_{2} x_{i 2} + \dots + β_{p} x_{i p}$

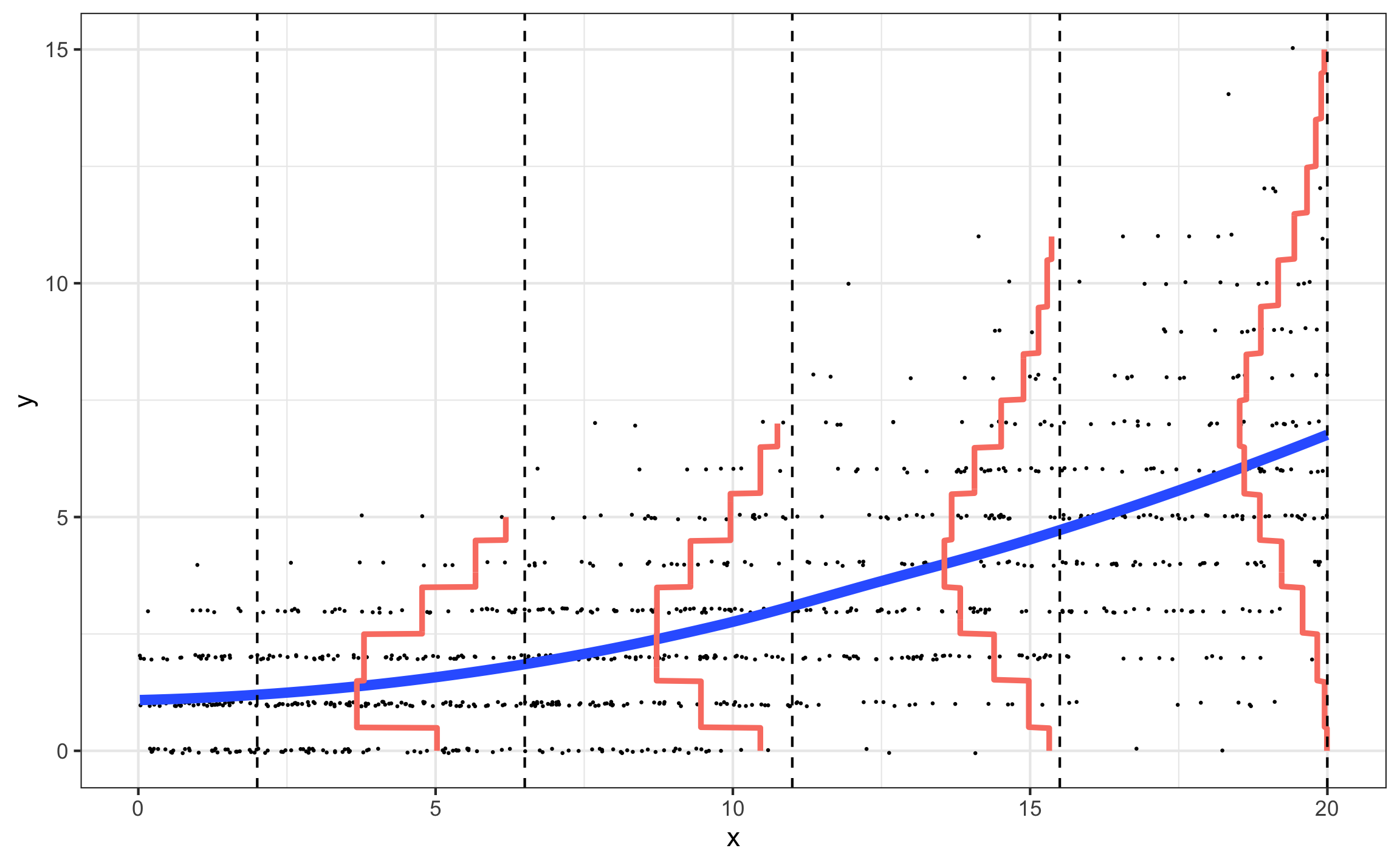
Each observation can have a different value of $λ$ based on its value of the predictors $x_{1}, \dots, x_{p}$
$λ$ determines the mean and variance, so we don’t need to estimate a separate error term

Poisson vs. multiple linear regression

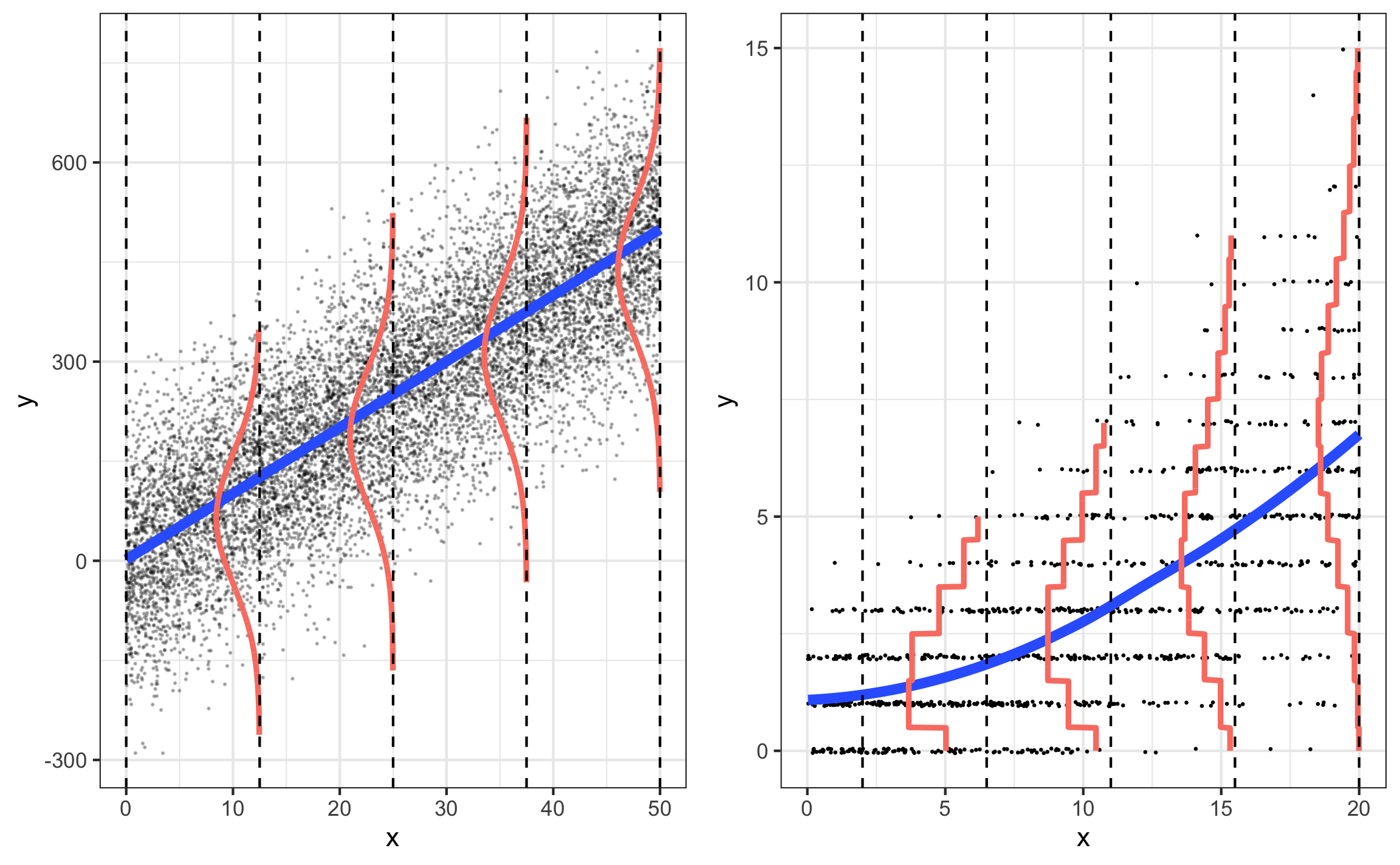
Regression models: Linear regression (left) and Poisson regression (right).

Assumptions for Poisson regression

Poisson response: The response variable is a count per unit of time or space, described by a Poisson distribution, at each level of the predictor(s)

Independence: The observations must be independent of one another

Mean = Variance: The mean must equal the variance

Linearity: The log of the mean rate, $\log (λ)$ , must be a linear function of the predictor(s)

Model 1: Household vs. Age

model1 <- glm(total ~ age, data = hh_data, family = poisson)

tidy(model1) |> 
  kable(digits = 4)

term	estimate	std.error	statistic	p.value
(Intercept)	1.5499	0.0503	30.8290	0
age	-0.0047	0.0009	-5.0258	0

$\log (\hat{λ}) = 1.5499 - 0.0047 a g e$

The coefficient for age is -0.0047. Interpret this coefficient in context. Select all that apply.

The mean household size is predicted to decrease by 0.0047 for each year older the head of the household is.
The mean household size is predicted to multiply by a factor of 0.9953 for each year older the head of the household is.
The mean household size is predicted to decrease by 0.9953 for each year older the head of the household is.
The mean household size is predicted to multiply by a factor of 0.47% for each year older the head of the household is.
The mean household size is predicted to decrease by 0.47% for each year older the head of the household is.

Is the coefficient of `age` statistically significant?

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	1.5499	0.0503	30.8290	0	1.4512	1.6482
age	-0.0047	0.0009	-5.0258	0	-0.0065	-0.0029

$H_{0} : β_{1} = 0 vs. H_{a} : β_{1} \neq 0$

Test statistic

$Z = \frac{{\hat{β}}_{1} - 0}{S E ({\hat{β}}_{1})} = \frac{- 0.0047 - 0}{0.0009} = - 5.026 (using exact values)$

P-value

$P (| Z | > | - 5.026 |) = 5.01 \times 10^{- 7} \approx 0$

What are plausible values for the coefficient of `age`?

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	1.5499	0.0503	30.8290	0	1.4512	1.6482
age	-0.0047	0.0009	-5.0258	0	-0.0065	-0.0029

95% confidence interval for the coefficient of age

${\hat{β}}_{1} \pm z^{*} \times S E ({\hat{β}}_{1})$

where $z^{*} \sim N (0, 1)$ $- 0.0047 \pm 1.96 \times 0.0009 = (- .0065, - 0.0029)$

Interpret the interval in terms of the change in mean household size.

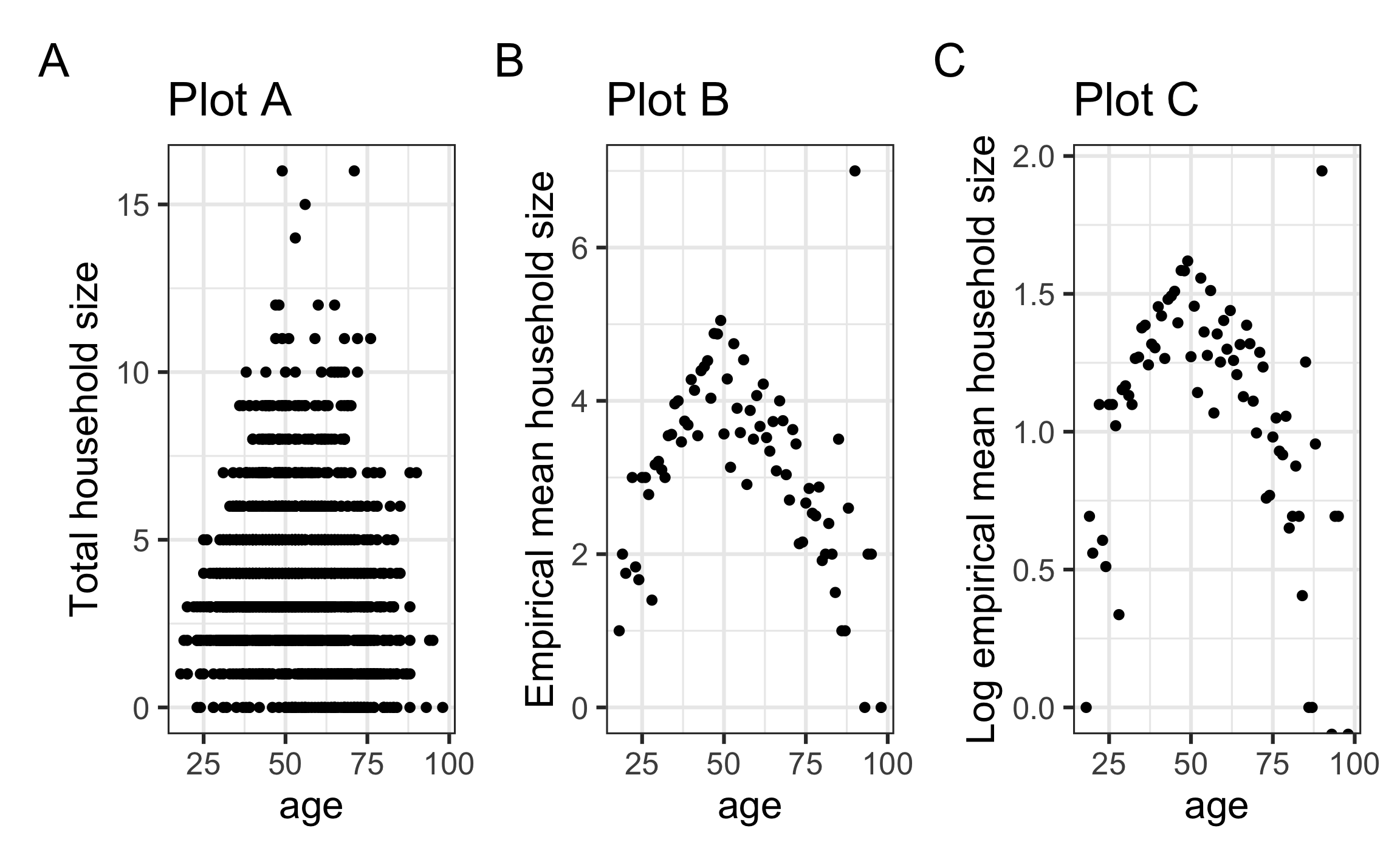
Which plot can best help us determine whether Model 1 is a good fit?

Model 2: Add a quadratic effect for `age`

hh_data <- hh_data |> 
  mutate(age2 = age*age)

model2 <- glm(total ~ age + age2, data = hh_data, family = poisson)
tidy(model2, conf.int = T) |> 
  kable(digits = 4)

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	-0.3325	0.1788	-1.8594	0.063	-0.6863	0.0148
age	0.0709	0.0069	10.2877	0.000	0.0575	0.0845
age2	-0.0007	0.0001	-11.0578	0.000	-0.0008	-0.0006

Model 2: Add a quadratic effect for `age`

term	estimate	std.error	statistic	p.value	conf.low	conf.high
(Intercept)	-0.3325	0.1788	-1.8594	0.063	-0.6863	0.0148
age	0.0709	0.0069	10.2877	0.000	0.0575	0.0845
age2	-0.0007	0.0001	-11.0578	0.000	-0.0008	-0.0006

We can determine whether to keep $a g e^{2}$ in the model in two ways:

1️⃣ Use the p-value (or confidence interval) for the coefficient (since we are adding a single term to the model)

2️⃣ Conduct a drop-in-deviance test

Deviance

A deviance is a way to measure how the observed data differs (deviates) from the model predictions.

It’s a measure unexplained variability in the response variable (similar to SSE in linear regression )
Lower deviance means the model is a better fit to the data

We can calculate the “deviance residual” for each observation in the data (more on the formula later). Let $({deviance residual}_{i}$ be the deviance residual for the $i^{t h}$ observation, then

$deviance = \sum (deviance residual)_{i}^{2}$

Note: Deviance is also known as the “residual deviance”

Drop-in-Deviance Test

We can use a drop-in-deviance test to compare two models. To conduct the test

1️⃣ Compute the deviance for each model

2️⃣ Calculate the drop in deviance

$drop-in-deviance = Deviance(reduced model) - Deviance(larger model)$

3️⃣ Given the reduced model is the true model $(H_{0} true)$ , then $drop-in-deviance \sim χ_{d}^{2}$

where $d$ is the difference in degrees of freedom between the two models (i.e., the difference in number of terms)

Drop-in-deviance to compare Model1 and Model2

anova(model1, model2, test = "Chisq") |>
  kable(digits = 3)

Resid. Df	Resid. Dev	Df	Deviance	Pr(>Chi)
1498	2337.089	NA	NA	NA
1497	2200.944	1	136.145	0

Write the null and alternative hypotheses.
What does the value 2337.089 tell you?
What does the value 1 tell you?
What is your conclusion?

Add `location` to the model?

Suppose we want to add location to the model, so we compare the following models:

Model A: $λ_{i} = β_{0} + β_{1} a g e_{i} + β_{2} a g e_{i}^{2}$

Model B: $λ_{i} = β_{0} + β_{1} a g e_{i} + β_{2} a g e_{i}^{2} + β_{3} L o c 1_{i} + β_{4} L o c 2_{i} + β_{5} L o c 3_{i} + β_{6} L o c 4_{i}$

Which of the following are reliable ways to determine if location should be added to the model?

Drop-in-deviance test
Use the p-value for each coefficient
Likelihood ratio test
Nested F Test
BIC

Looking ahead

For next time - Chapter 4 - Poisson Regression
- Sections 4.6, 4.10

References

Roback, Paul, and Julie Legler. 2021. Beyond multiple linear regression: applied generalized linear models and multilevel models in R. CRC Press.

Poisson Regression

Computing set up

Topics

Scenarios to use Poisson regression

Scenarios to use Poisson regression

Poisson distribution

Example¹

Poisson regression

The data: Household size in the Philippines

The data

Response variable

Why the least-squares model doesn’t work

Poisson regression model

Poisson vs. multiple linear regression

Assumptions for Poisson regression

Model 1: Household vs. Age

Is the coefficient of `age` statistically significant?

What are plausible values for the coefficient of `age`?

Which plot can best help us determine whether Model 1 is a good fit?

Model 2: Add a quadratic effect for `age`

Model 2: Add a quadratic effect for `age`

Deviance

Drop-in-Deviance Test

Drop-in-deviance to compare Model1 and Model2

Add `location` to the model?

Looking ahead

References