Lecture 14 AE: Modeling two-level longitudinal data

Published

March 4, 2024

library(tidyverse)
library(knitr)
library(lme4)
library(broom.mixed)
library(skimr)
charter <- read_csv("data/charter-long.csv") |>
  mutate(urban = factor(urban),
         charter = factor(charter))

Exploratory data analysis

Caution

This is not a complete EDA for this data.

Univariate EDA

ggplot(data = charter, aes(x = MathAvgScore))  + 
  geom_histogram(fill = "steelblue", color = "black") + 
  labs(title = "Average math scores", 
  subtitle = "6th graders in Minneapolis public schools")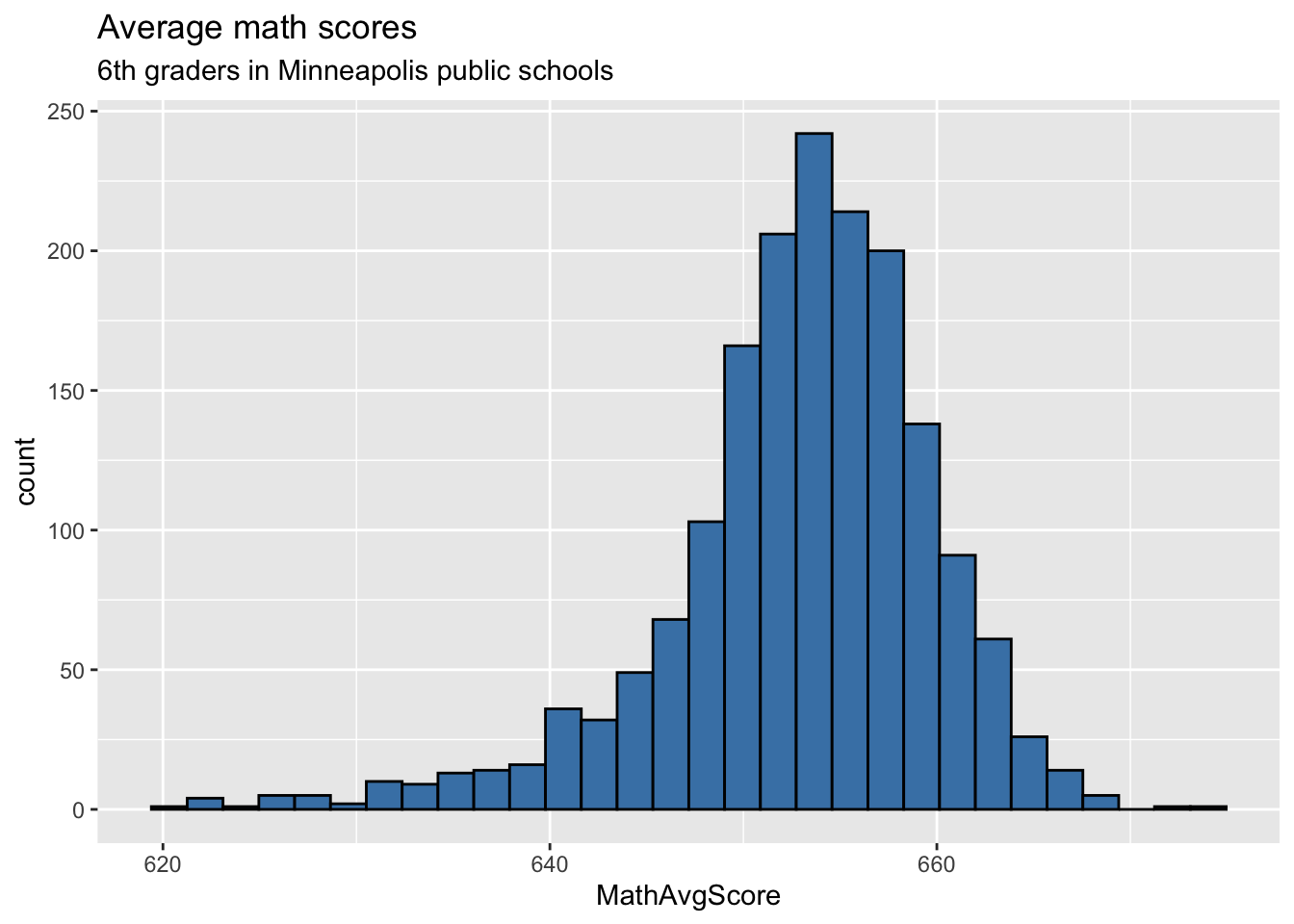

Bivariate EDA

ggplot(data = charter, aes(x = charter, y = MathAvgScore)) + 
  geom_boxplot(fill = "steelblue", color = "black")  +
  labs(title = "Average math scores of 6th graders in Minneapolis public schools", 
       subtitle = "by school type")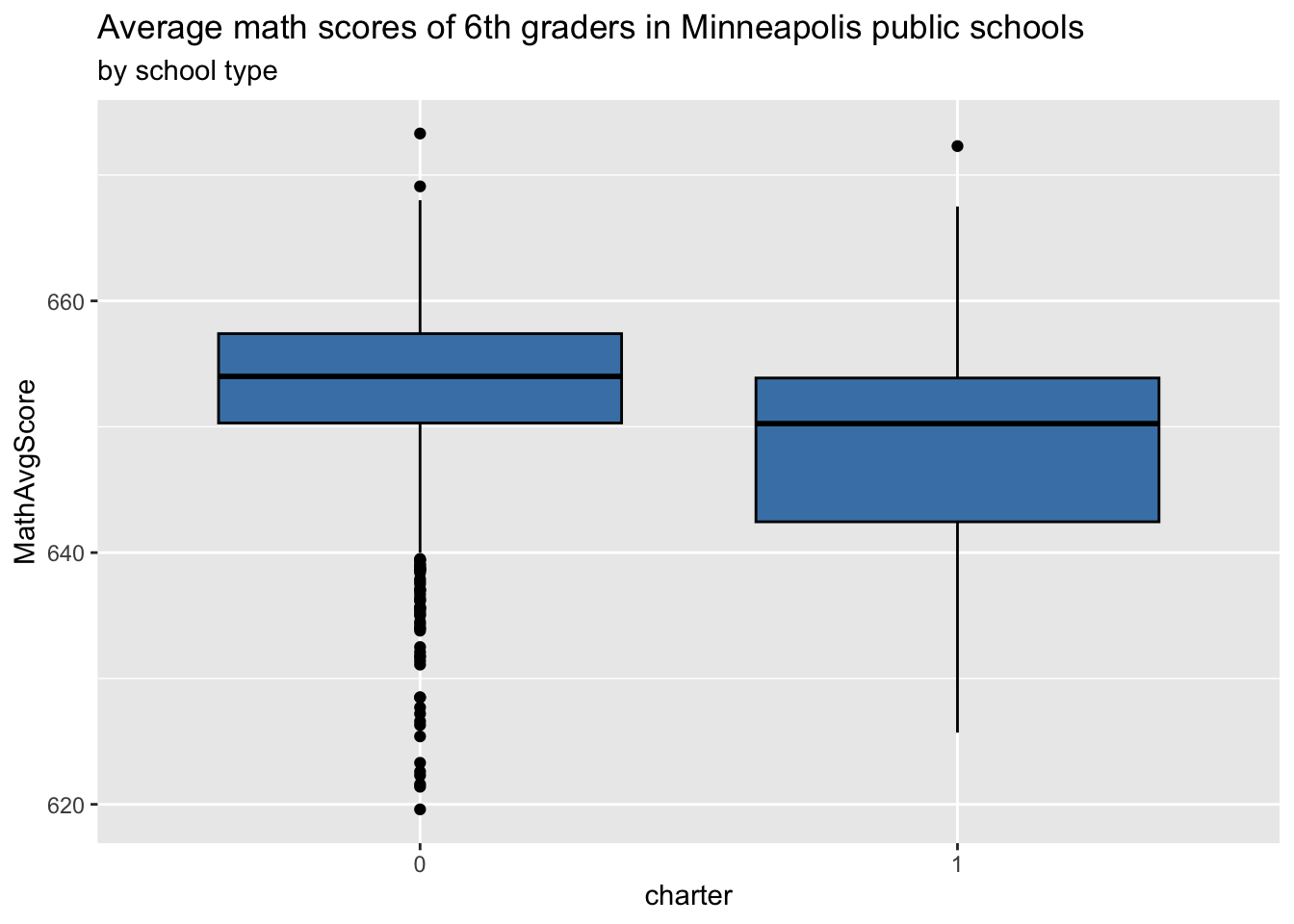

Ex 1

Make a scatterplot of the average math score versus the proportion of students who receive free or reduced lunches in a school (based on 2010 figures).

## scatterplot
Ex 2

What do you observe from each bivariate plot?

Lattice plot

Make a lattice plot of the average math scores over time for 24 randomly selected schools.

set.seed(030424)

# get sample of 24 schools
sample_schools <- charter |>
  distinct(schoolid) |>
  sample_n(24) |> pull()

# get data for those schools
sample_data <- charter |>
  filter(schoolid %in% sample_schools)
## lattice plot

Spaghetti plots

Plot average math scores over time for each school. Apply a LOESS smoother (locally estimated scatterplot smoother).

ggplot(data = charter, aes(x = year08, y = MathAvgScore)) + 
  geom_line(aes(group = schoolid), color = "light gray") + 
  geom_smooth(color = "black", linewidth = 1, method = "loess") + 
  labs(x ="Years since 2008",
       y ="Average Math Scores", 
       title = "Math Scores over time for 6th graders in Minneapolis public schools")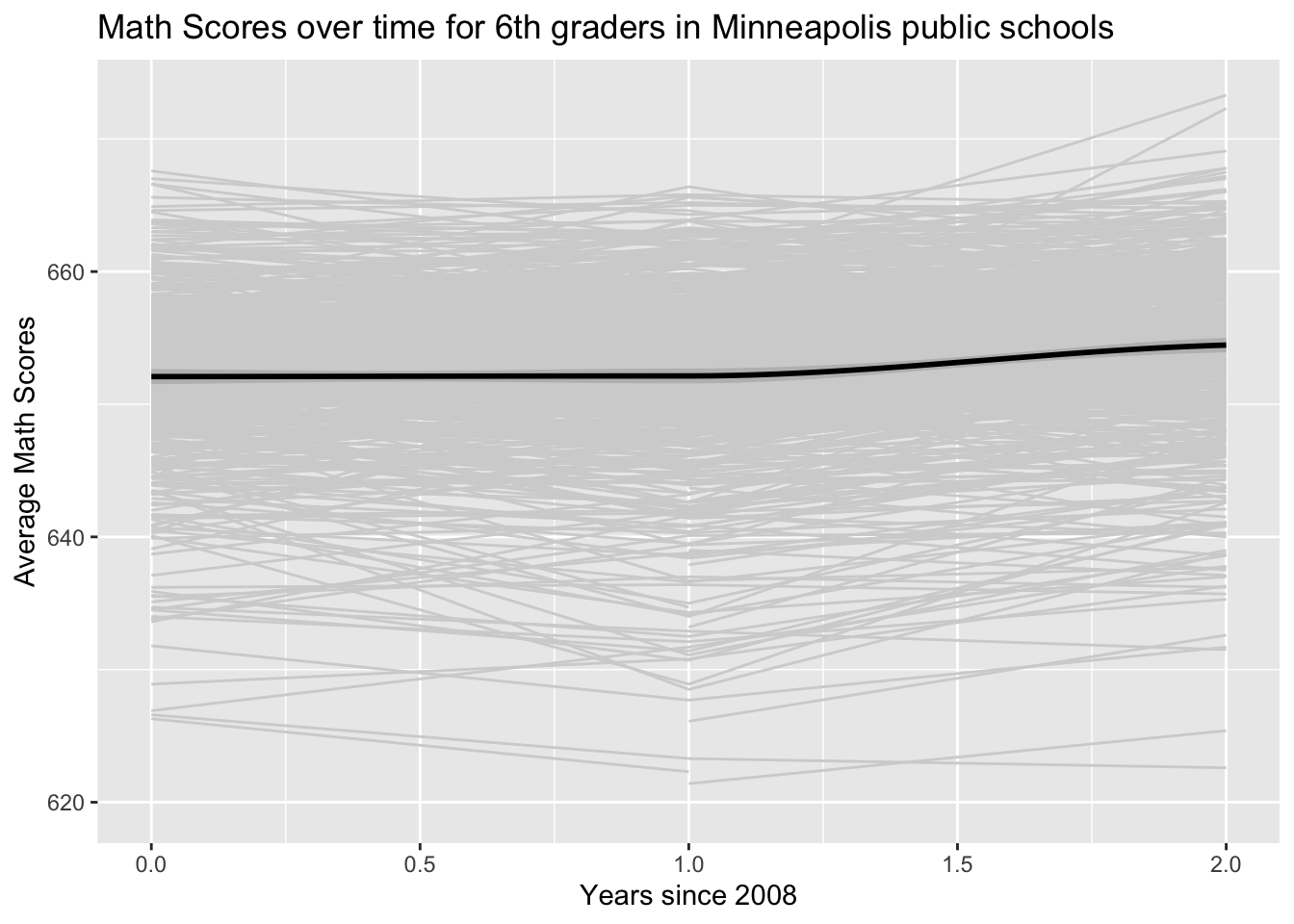

Ex 3

  • What features are easier to observe in the lattice plots versus the spaghetti plot?

  • What features are easier to observe in the spaghetti plot versus the lattice plot?

Ex 4
  • Make a separate spaghetti plot of average maths scores over time by school type (charter vs. non-charter).
# spaghetti plot by school type
Ex 5

  • How do the typical math scores from charter and non-charter schools compare over time?

  • How does the variability in math scores from charter and non-charter schools compare over time?

Unconditional means model

Ex 6

Fit the unconditional means model and calculate the intraclass correlation.

# Fit the unconditional means model
# Calculate the intraclass correlation

Unconditional growth model

Ex 7

Fit the unconditional growth model.

# Fit the unconditional growth model
Ex 8

Calculate the \(Pseudo R^2\) to estimate the change of within school variance between the unconditional means and unconditional growth models.

# Pseudo R^2

Model with school-level covariates

Ex 9

Fit the model with the school-level covariates.

# Fit model with school level covariates