Lecture 11: Multilevel models

library(tidyverse)
library(broom)
library(knitr)
library(patchwork)

music <- read_csv("data/musicdata.csv") |>
  mutate(orchestra = factor(if_else(instrument == "orchestral instrument", 
                                    1, 0)), 
         large_ensemble = factor(if_else(perform_type == "Large Ensemble", 
                                         1, 0))
  )

Part 1: Univariate EDA

Below are plots of the distribution of the response variable na for (1) individual performances and (2) aggregated by musician (id)

p1 <- ggplot(data = music, aes(x = na)) + 
  geom_histogram(color = "white", binwidth = 2) + 
  labs(x = "NA", 
       title = "Individual performances")

p2 <- music |>
  group_by(id) |>
  summarise(mean_na = mean(na)) |>
  ggplot(aes(x = mean_na)) + 
  geom_histogram(color = "white", binwidth = 2) + 
  labs(x = "Average NA",
       title = "Aggregated by musician")

p1 + p2 + plot_annotation(title = "Negative affect scores")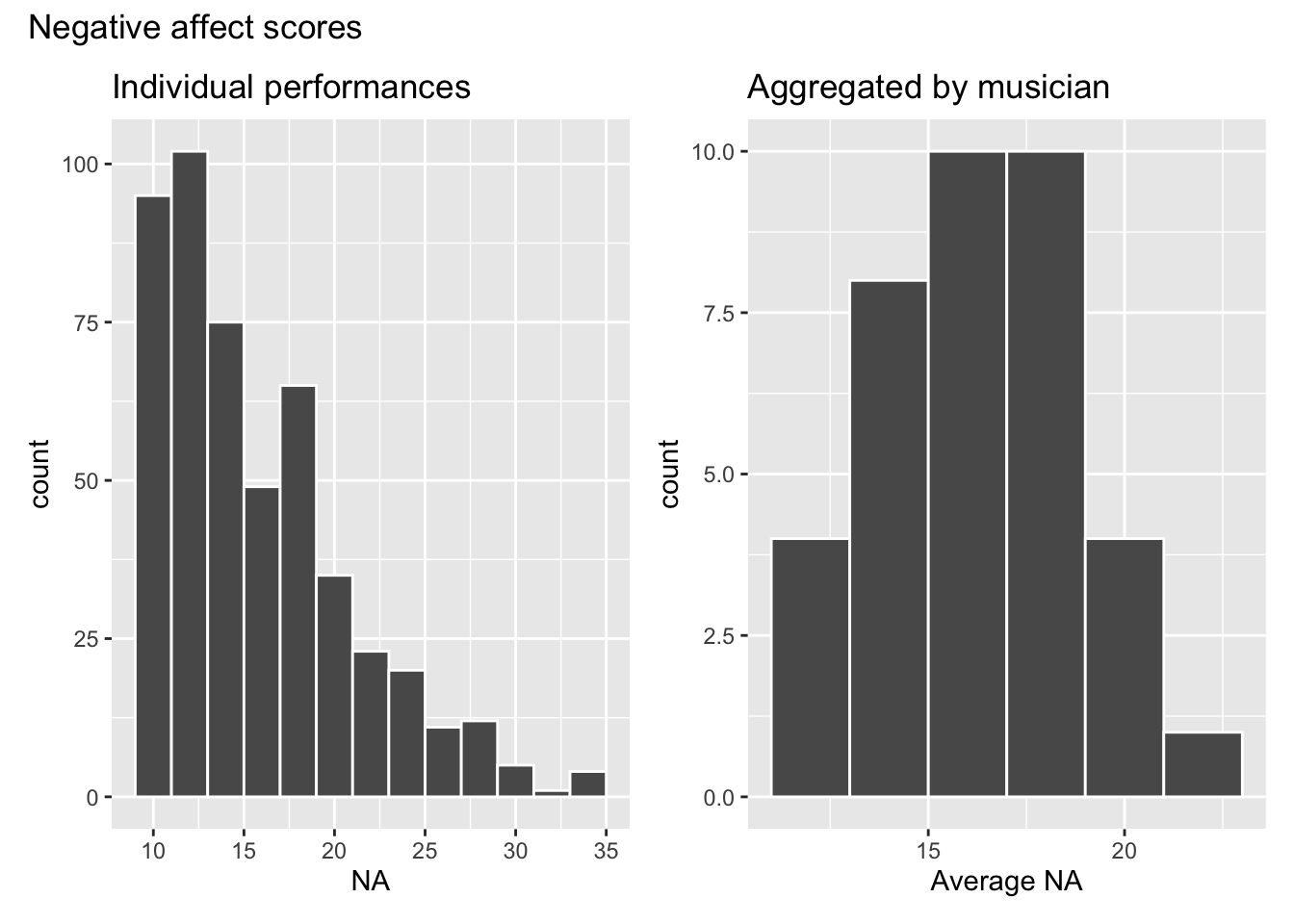

Ex 1

How are the plots similar? How do they differ?

Ex 2

What are some advantages of each plot? What are some disadvantages?

Part 2: Bivariate EDA

Ex 3

Make a single scatterplot of the negative affect versus number of previous performances (previous) using the individual observations. Use geom_smooth() to add a linear regression line to the plot.

# add code

Ex 4

Make a separate scatterplot of negative affect versus number of previous performances (previous) for each musician (id). Use geom_smooth() to add a linear regression line to each plot.

# add code

Ex 5

How are the plots similar? How do they differ?

Ex 6

What are some advantages of each plot? What are some disadvantages?

Part 3: Level One Models

Fit and display the Level One model for musician 22.

music |>
  filter(id == 22) |>
  lm(na ~ large_ensemble, data = _) |>
  tidy() |>
  kable(digits = 3)

term	estimate	std.error	statistic	p.value
(Intercept)	24.500	1.96	12.503	0.000
large_ensemble1	-7.833	2.53	-3.097	0.009

Fit the Level One models to obtain the fitted slope, intercept, and $R^2$ value for each musician.

# set up tibble for fitted values
model_stats <- tibble(slopes = rep(NA,37), 
               intercepts = rep(NA,37), 
               r.squared = rep(NA, 37))

ids <- music |> distinct(id) |> pull()

# fit the model and score the releveant statistcs
for(i in 1:length(ids)){
level_one_data <- music |>
  filter(id == ids[i]) 

# check if more than one performance type 
num_perform_types <- level_one_data |> 
  distinct(large_ensemble) |> 
  nrow() 

if(num_perform_types > 1){
  #if more than one performance type, calculate all model statistics

level_one_model <- lm(na ~ large_ensemble, 
                      data = level_one_data)

level_one_model_tidy <- tidy(level_one_model)

model_stats$slopes[i] <- level_one_model_tidy$estimate[2]
model_stats$intercepts[i] <- level_one_model_tidy$estimate[1]
model_stats$r.squared[i] <- glance(level_one_model)$r.squared
}else{
  # if only one performance type, calculate intercept and R^2
  model_stats$intercepts[i] <- mean(level_one_data$na)
  model_stats$r.squared[i] <- 0
}
}

Plot the estimated intercepts, slopes and, $R^2$ values.

level_one_int <- ggplot(model_stats, aes(x = intercepts)) + 
  geom_histogram(color = "white", binwidth = 2) +
  labs(x = "", 
       title = "Fitted intercepts", 
       subtitle = "for 37 musicians")

level_one_slope <- ggplot(model_stats, aes(x = slopes)) + 
  geom_histogram(color = "white", binwidth = 2) +
  labs(x = "", 
       title = "Fitted slopes", 
       subtitle = "for 37 musicians")

level_one_int + level_one_slope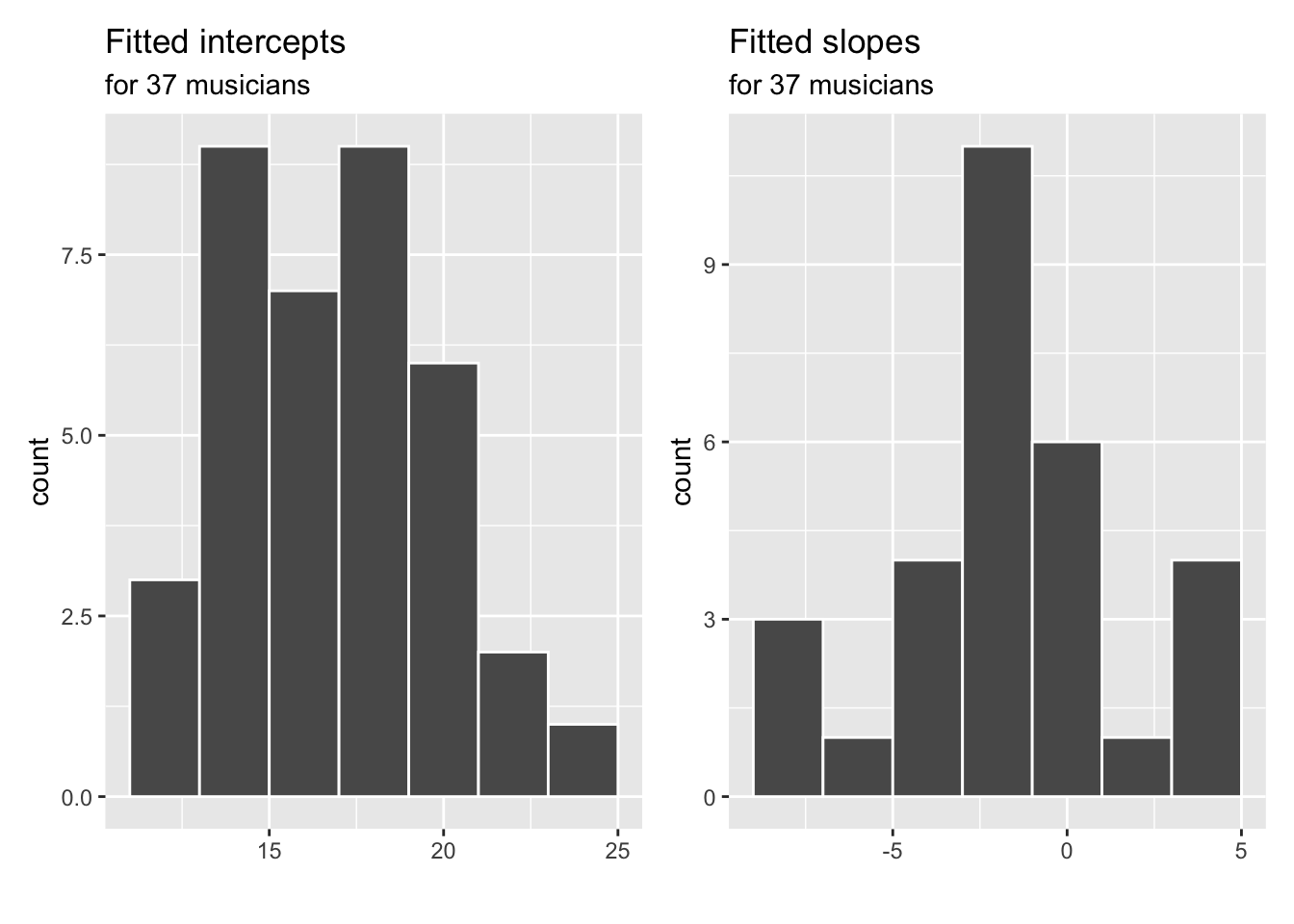

ggplot(model_stats, aes(x = r.squared)) + 
  geom_histogram(color = "white", binwidth = 0.05) +
  labs(x = "", 
       title = "Fitted R-squared values", 
       subtitle = "for 37 musicians")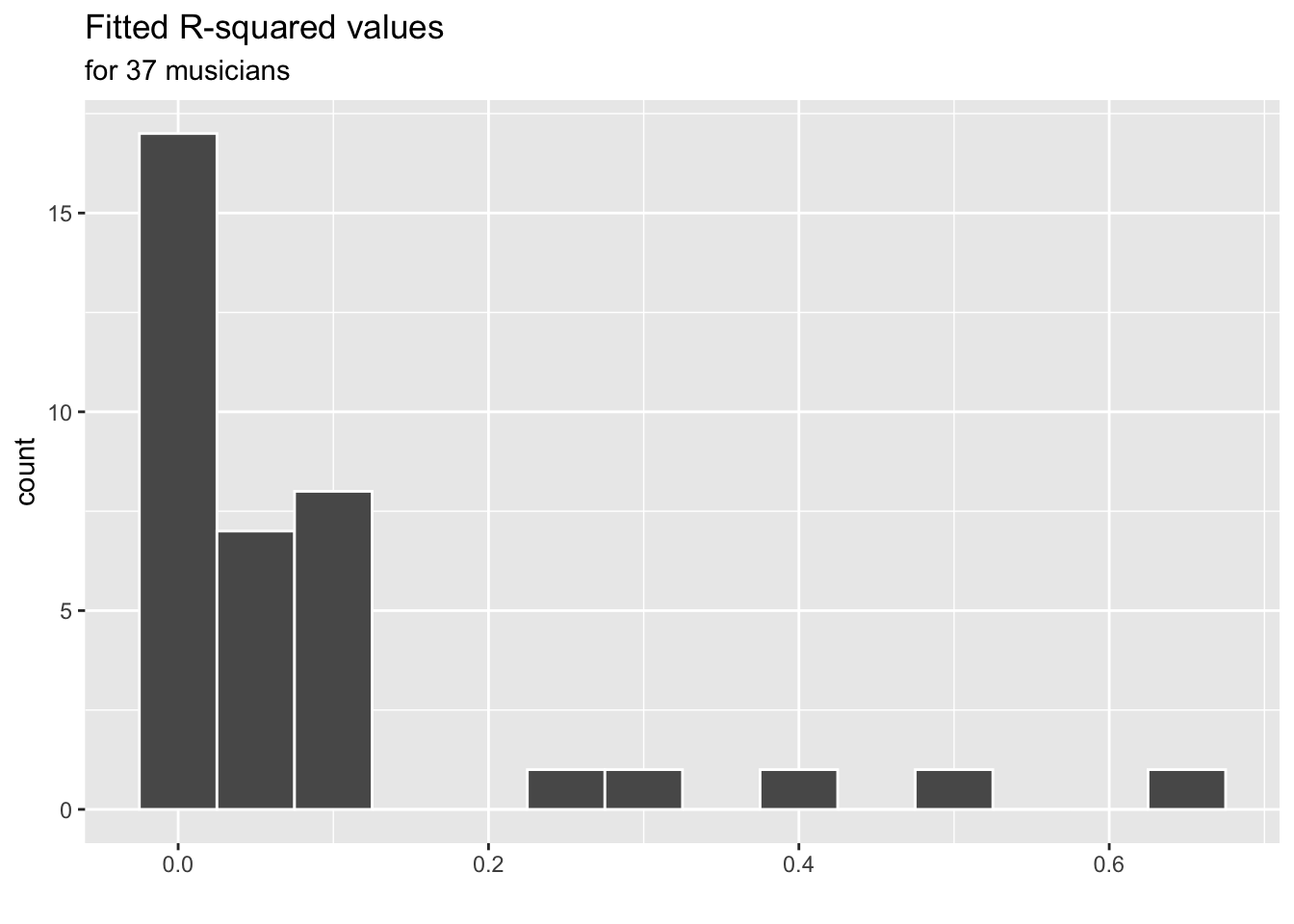

Part 4: Level Two Models

# Make a Level Two data set
musicians <- music |>
  distinct(id, orchestra) |>
  bind_cols(model_stats)

Model for intercepts

a <- lm(intercepts ~ orchestra, data = musicians) 
tidy(a) |>
  kable(digits = 3)

term	estimate	std.error	statistic	p.value
(Intercept)	16.283	0.671	24.249	0.000
orchestra1	1.411	0.991	1.424	0.163

Model for slopes

b <- lm(slopes ~ orchestra, data = musicians) 
tidy(b) |>
  kable(digits = 3)

term	estimate	std.error	statistic	p.value
(Intercept)	-0.771	0.851	-0.906	0.373
orchestra1	-1.406	1.203	-1.168	0.253